Full solution
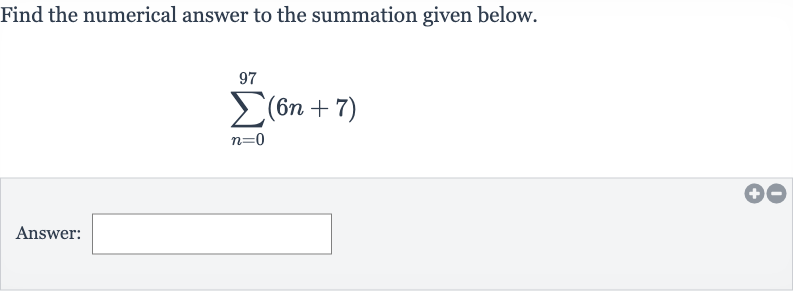
Q. Find the numerical answer to the summation given below.Answer:
- Identify Common Difference and Terms: We need to find the sum of the arithmetic series given by the formula . To do this, we will first identify the common difference and the number of terms in the series.The common difference is , and since we are starting from and going up to , there are terms in total.
- Split Summation into Two Parts: We can split the summation into two separate summations: one for the term and one for the constant . This gives us .
- Calculate Sum of n Terms: Let's first calculate the sum of the terms. The sum of an arithmetic series can be found using the formula . The first term when is and the last term when is . So we have .
- Calculate Sum of Constant Terms: Performing the calculation for the sum of the terms, we get .
- Add Two Sums for Total: Now we calculate the sum of the constant terms. Since this is a constant added times, the sum is simply .
- Add Two Sums for Total: Now we calculate the sum of the constant terms. Since this is a constant added times, the sum is simply .Performing the calculation for the sum of the constant terms, we get .
- Add Two Sums for Total: Now we calculate the sum of the constant terms. Since this is a constant added times, the sum is simply .Performing the calculation for the sum of the constant terms, we get .Finally, we add the two sums together to get the total sum of the series: .
- Add Two Sums for Total: Now we calculate the sum of the constant terms. Since this is a constant added times, the sum is simply .Performing the calculation for the sum of the constant terms, we get .Finally, we add the two sums together to get the total sum of the series: .Adding the two sums, we get . This is the sum of the series from to of the expression .