Full solution
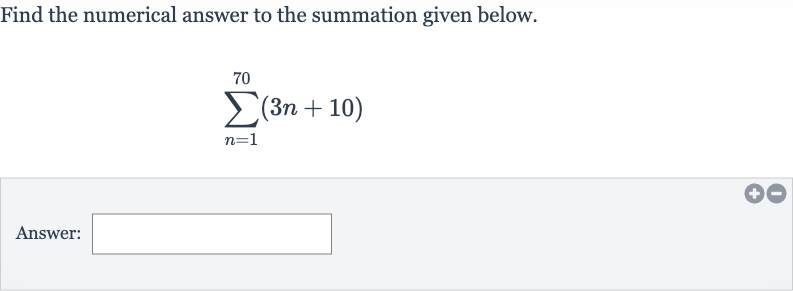
Q. Find the numerical answer to the summation given below.Answer:
- Recognize Split Summations: Recognize that the summation of the series can be split into two separate summations: the summation of from to and the summation of from to . This can be written as .
- Calculate Summation: Calculate the first summation . This is an arithmetic series where each term is times the corresponding term of the sum of the first natural numbers. The sum of the first natural numbers is given by the formula . Therefore, the sum of from to is .
- Calculate Sum: Perform the calculation from Step . .
- Calculate Summation: Calculate the second summation . Since is a constant, the sum is simply added to itself times, which is .
- Calculate Sum: Perform the calculation from Step . .
- Find Total Sum: Add the results from Step and Step to find the total sum of the series. .