Full solution
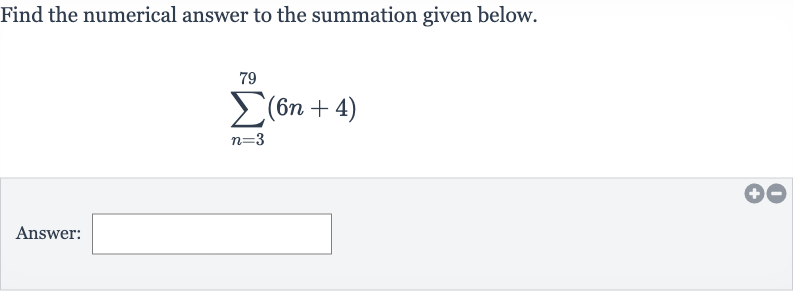
Q. Find the numerical answer to the summation given below.Answer:
- Split Summation: Recognize that the summation of the series can be split into two separate summations, one for and one for . This gives us .
- Evaluate First Term: Evaluate the first term . This is an arithmetic series, and the sum of an arithmetic series can be found using the formula , where is the number of terms, is the first term, and is the last term. The first term when is , and the last term when is . The number of terms is .
- Calculate First Term Sum: Calculate the sum of the first term using the arithmetic series sum formula.
- Evaluate Second Term: Evaluate the second term . This is a constant series, and the sum of a constant series is simply the constant times the number of terms. We already found the number of terms to be in Step .
- Calculate Second Term Sum: Calculate the sum of the second term .
- Add Results: Add the results from Step and Step to get the final answer.Total Sum = =