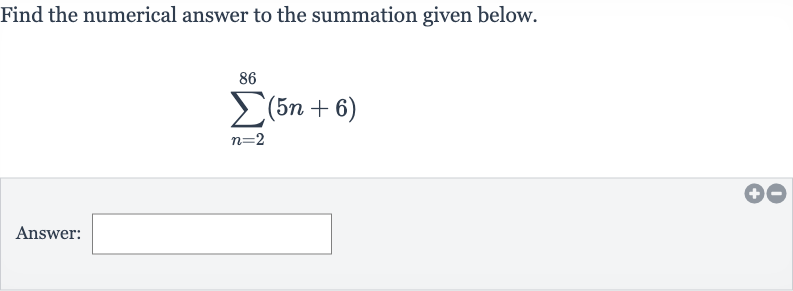
Find the numerical answer to the summation given below. sum_(n=2)^(86)(5n+6) Answer:

Question

Find the numerical answer to the summation given below.  sum_(n=2)^(86)(5n+6) Answer:

Bytelearn · Accepted Answer

Split Summation: Recognize that the summation of the series can be split into two separate summations: the summation of 5n from n=2 to n=86 and the summation of 6 from n=2 to n=86. This can be written as sum_(n=2)^(86)(5n) + sum_(n=2)^(86)(6).Calculate Arithmetic Series: Calculate the first part of the summation, sum_(n=2)^(86)(5n). This is an arithmetic series where each term is 5 times n. The sum of an arithmetic series can be found using the formula S = n/2 * (a_1 + a_n), where n is the number of terms, a_1 is the first term, and a_n is the last term. First, we need to find the number of terms in the series, which is 86 - 2 + 1 = 85. The first term when n=2 is 5*2 = 10, and the last term when n=86 is 5*86 = 430. Now we can calculate the sum: S = 85/2 * (10 + 430).Calculate Constant Series: Perform the calculation from Step 2. S = 85/2 * 440 = 85 * 220 = 18700. This is the sum of the first part of the series.Add Results: Calculate the second part of the summation, sum_(n=2)^(86)(6). This is a constant series where each term is 6. The sum of a constant series is simply the constant times the number of terms. We already found the number of terms to be 85 in Step 2. So the sum is 85 * 6.Calculate Total Sum: Perform the calculation from Step 4. The sum is 85 * 6 = 510. This is the sum of the second part of the series.Verify Calculations: Add the results from Step 3 and Step 5 to find the total sum of the series. The total sum is 18700 + 510 = 19210.Verify the calculations to ensure there are no math errors. Rechecking the arithmetic and the application of formulas confirms that the calculations are correct.

Find the numerical answer to the summation given below. $\newline$ $\sum_{n=2}^{86}(5 n+6)$ $\newline$ Answer:

Full solution

More problems from Sum of finite series starts from 1

Related topics

Find the numerical answer to the summation given below.\newline∑n=286(5n+6) \sum_{n=2}^{86}(5 n+6) n=2∑86​(5n+6)\newlineAnswer:

Find the numerical answer to the summation given below. $\newline$ $\sum_{n=2}^{86}(5 n+6)$ $\newline$ Answer: