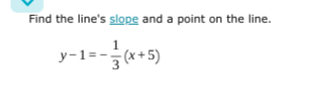Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the line's slope and a point on the line. y-1=-(1)/(3)(x+5)

Find the line's slope and a point on the line.\newliney−1=−13(x+5) y-1=-\frac{1}{3}(x+5)

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Roots of rational numbersright chevron icon

Full solution

Q. Find the line's slope and a point on the line.\newliney−1=−13(x+5) y-1=-\frac{1}{3}(x+5)
  1. Rewrite equation: Rewrite the equation in slope-intercept form y=mx+by = mx + b to identify the slope and y-intercept.\newliney−1=−(13)(x+5)y - 1 = -\left(\frac{1}{3}\right)(x + 5)\newliney=−(13)x−(13)(5)+1y = -\left(\frac{1}{3}\right)x - \left(\frac{1}{3}\right)(5) + 1\newliney=−(13)x−53+1y = -\left(\frac{1}{3}\right)x - \frac{5}{3} + 1\newliney=−(13)x−23y = -\left(\frac{1}{3}\right)x - \frac{2}{3}
  2. Identify slope: Identify the slope mm from the equation y=mx+by = mx + b.\newlineSlope mm = −13-\frac{1}{3}
  3. Identify point: Identify a point on the line using the y-intercept ( extit{b}).\newlineThe y-intercept is at y=−23y = -\frac{2}{3} when x=0x = 0.\newlineSo, the point (0,−23)(0, -\frac{2}{3}) is on the line.

More problems from Roots of rational numbers

Question
Find the real-number root. \newline16\sqrt{16}\newline\newlineWrite your answer in simplified form. \newline____\_\_\_\_
Get tutor helpright-arrow

Posted 3 months ago

Question
Find the real-number root. \newline916\sqrt{\frac{9}{16}}\newlineSimplify your answer and write it as a decimal or as a proper or improper fraction.\newline_____\_\_\_\_\_
Get tutor helpright-arrow

Posted 3 months ago

Question
Find the real-number root using a calculator. Round your answer to the nearest thousandth. \newline`\sqrt{957} `\newline _______
Get tutor helpright-arrow

Posted 3 months ago

Question
Multiply. Write your answer in simplest form. \newline273×42\sqrt{273} \times \sqrt{42}\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Simplify. \newline634\sqrt{\frac{63}{4}}\newline______
Get tutor helpright-arrow

Posted 3 months ago

Question
Simplify. Rationalize the denominator.\newline−49−2\frac{-4}{9 - \sqrt{2}}\newline______
Get tutor helpright-arrow

Posted 3 months ago

Question
Solve for z z .\newline16=z 16 = \sqrt{z} \newlinez= z = _____
Get tutor helpright-arrow

Posted 3 months ago

Question
Simplify the radical expression. 14x14 \sqrt{14x^{14}} Write your answer in the form A A , B \sqrt{B} , or AB A\sqrt{B} , where A A and B B are constants or expressions in x x . Use at most one radical in your answer, and at most one absolute value symbol in your expression for A A . ______
Get tutor helpright-arrow

Posted 3 months ago

Question
Simplify the radical expression.\newline12x12\sqrt{12x^{12}}\newlineWrite your answer in the form AA, B\sqrt{B}, or ABA\sqrt{B}, where AA and BB are constants or expressions in xx. Use at most one radical in your answer, and at most one absolute value symbol in your expression for AA.\newline‾\underline{\hspace{3cm}}
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the value of sin⁡(5π6)? \sin \left(\frac{5 \pi}{6}\right) ? \newlineChoose 11 answer:\newline(A) −32 -\frac{\sqrt{3}}{2} \newline(B) −22 -\frac{\sqrt{2}}{2} \newline(C) 12 \frac{1}{2} \newline(D) 150150
Get tutor helpright-arrow

Posted 4 months ago

View all (210)