AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
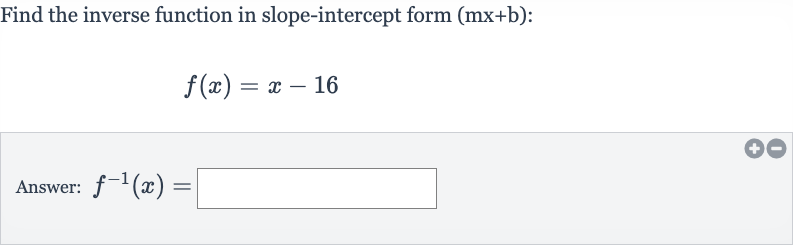
Find the inverse function in slope-intercept form :Answer:
Full solution
Q. Find the inverse function in slope-intercept form :Answer:
- Understand Inverse Function: Understand the concept of an inverse function. An inverse function reverses the operation of the original function. If , then . To find the inverse function, we need to solve for in terms of .
- Replace with : Replace with to prepare for finding the inverse.
- Swap x and y: Swap and to find the inverse function.
- Solve for y: Solve for y to get the inverse function in slope-intercept form.
- Replace with : Replace with to denote the inverse function.
More problems from Find the vertex of the transformed function
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
