AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
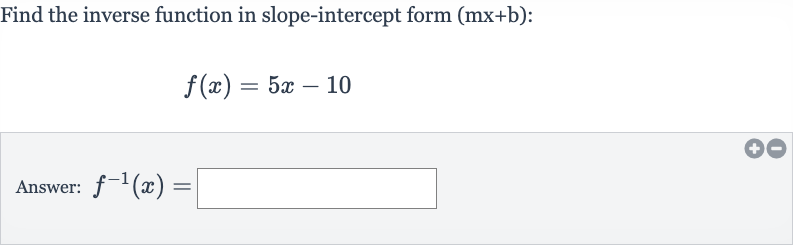
Find the inverse function in slope-intercept form :Answer:
Full solution
Q. Find the inverse function in slope-intercept form :Answer:
- Understand Inverse Function: Understand the concept of an inverse function. An inverse function, denoted as , swaps the and values of the original function. For the function , we want to find a function that will give us the original value when we input the value from .
- Replace with : Replace with to make the equation easier to work with.
- Swap x and y: Swap x and y to find the inverse function.
- Solve for y: Solve for y to get the inverse function in slope-intercept form.
- Simplify Inverse Function: Simplify the inverse function if necessary. This is the inverse function in slope-intercept form.
More problems from Find the vertex of the transformed function
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
