AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
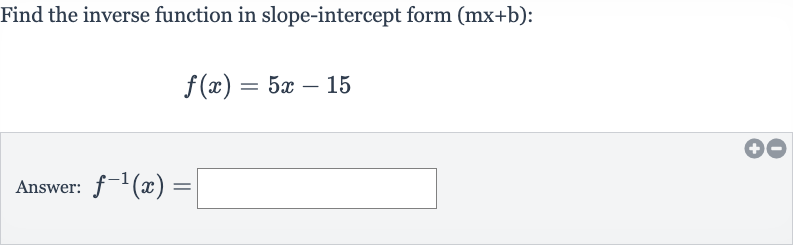
Find the inverse function in slope-intercept form :Answer:
Full solution
Q. Find the inverse function in slope-intercept form :Answer:
- Understand Inverse Function: Understand the concept of an inverse function. An inverse function essentially reverses the operation of the original function. If , then . To find the inverse function, we need to solve for in terms of .
- Replace with : Replace with to make the equation easier to work with.
- Swap x and y: Swap x and y to find the inverse function.
- Solve for y: Solve for y in terms of x.Add to both sides of the equation to isolate the term with on one side.
- Divide and Solve: Divide both sides by to solve for .
- Write in Slope-Intercept Form: Write the inverse function in slope-intercept form.
More problems from Find the vertex of the transformed function
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
