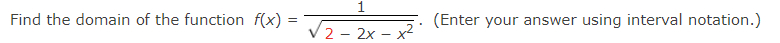Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the domain of the function
f(x)=(1)/(sqrt(2-2x-x^(2))). (Enter your answer using interval notation.)

Find the domain of the function $f(x)=\frac{1}{\sqrt{2-2 x-x^{2}}}$ . (Enter your answer using interval notation.)

View step-by-step help

View step-by-step help

Domain and range of quadratic functions: equations

Full solution

Q. Find the domain of the function

f(x)=\frac{1}{\sqrt{2-2 x-x^{2}}}

. (Enter your answer using interval notation.)

Identify Inner Function: Identify the inner function within the square root to determine where it is non-negative, as the square root function requires non-negative inputs for real number outputs.
Rewrite in Standard Form: Rewrite the quadratic equation in standard form and identify values of $a$ , $b$ , and $c$ .
Check Discriminant: Use the discriminant formula, $b^2 - 4ac$ , to check if the quadratic equation has real roots, which will help in finding the intervals where the function under the square root is non-negative.
Solve for Roots: Since the discriminant is positive, solve for the roots of the equation using the quadratic formula, $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$ .
Determine Non-Negative Intervals: Determine the intervals where the function under the square root, $2 - 2x - x^2$ , is non-negative. This is between the roots because the parabola opens downwards ( $a = -1$ ).
Write Domain: Write the domain of $f(x)$ using interval notation, considering where the function under the square root is non-negative.

More problems from Domain and range of quadratic functions: equations

Question

Solve by completing the square.

\newline

m^2 - 10m - 29 = 0

\newline

Write your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.

\newline

`m` = ____ or `m` = _____

Posted 2 months ago

Question

g(x)

g(x)

is the translation

5

f(x)=x^2

\newline

Write your answer in the form

a(x–h)^2+k

a

h

k

\newline

g(x)=

Posted 2 months ago

Question

What is the range of this quadratic function?

\newline

y = x^2 - 4x + 4

\newline

\newline

\left\{y \mid y \geq 2\right\}

\newline

\left\{y \mid y \leq 0\right\}

\newline

\left\{y \mid y \geq 0\right\}

\newline

\text{all real numbers}

Posted 2 months ago

Question

Write the equation of the parabola that passes through the points

(1,0)

(2,0)

(3,\text{–}16)

. Write your answer in the form

y = a(x – p)(x – q)

a

p

q

are integers, decimals, or simplified fractions.

\newline

Posted 2 months ago

Question

Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.

\newline

f^2 + 8f + \_\_\_\_\_

Posted 2 months ago

Question

h

\newline

h^2 + 39h = 0

\newline

\newline

Write each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.

\newline

h =

\newline

Posted 2 months ago

Question

Write a quadratic function with zeros

-9

-7

\newline

Write your answer using the variable

x

and in standard form with a leading coefficient of

1

\newline

f(x) = \_\_\_\_\_

Posted 2 months ago

Question

Find the equation of the axis of symmetry for the parabola

y = x^2

\newline

Simplify any numbers and write them as proper fractions, improper fractions, or integers.

\newline

\underline{\hspace{3cm}}

Posted 3 months ago

Question

g(x)

g(x)

is the translation

8

f(x) = x^2

\newline

Write your answer in the form

a(x – h)^2 + k

a

h

k

\newline

g(x) =

\newline

Posted 3 months ago

Question

x

\newline

x^2 = 1

\newline

\newline

Write your answer in simplified, rationalized form.

\newline

x =

x =

\newline

Posted 3 months ago