Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the argument of the complex number
sqrt2-sqrt2i in the interval
0 <= theta < 2pi. Express your answer in terms of
pi.
Answer:

Find the argument of the complex number $\sqrt{2}-\sqrt{2} i$ in the interval $0 \leq \theta<2 \pi$ . Express your answer in terms of $\pi$ . $\newline$ Answer:

View step-by-step help

View step-by-step help

Find trigonometric ratios using a Pythagorean or reciprocal identity

Full solution

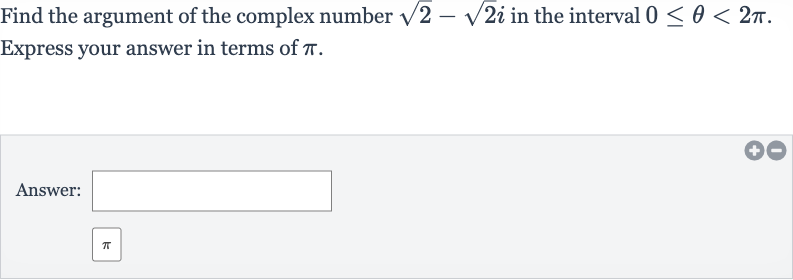
Q. Find the argument of the complex number

\sqrt{2}-\sqrt{2} i

in the interval

0 \leq \theta<2 \pi

. Express your answer in terms of

\pi

.

\newline

Answer:

Calculate Argument using atan $2$ : To find the argument of a complex number in the form $a + bi$ , where $a$ is the real part and $b$ is the imaginary part, we can use the formula $\theta = \text{atan2}(b, a)$ , where $\text{atan2}$ is the two-argument arctangent function that takes into account the signs of both arguments to determine the correct quadrant of the angle. $\newline$ For the complex number $\sqrt{2} - \sqrt{2}i$ , we have $a = \sqrt{2}$ and $b = -\sqrt{2}$ .
Identify Quadrant: We calculate the argument using the atan $2$ function: $\theta = \text{atan2}(-\sqrt{2}, \sqrt{2})$ . Since both the real and imaginary parts are equal in magnitude but opposite in sign, the argument is in the fourth quadrant.
Calculate Alpha: In the fourth quadrant, the argument of the complex number is $2\pi - \alpha$ , where $\alpha$ is the angle formed with the positive x-axis. Since the real and imaginary parts are equal in magnitude, $\alpha$ is $45$ degrees or $\pi/4$ radians.
Final Argument Calculation: Therefore, the argument $\theta$ is $2\pi - \frac{\pi}{4}$ , which simplifies to $\frac{7\pi}{4}$ .

More problems from Find trigonometric ratios using a Pythagorean or reciprocal identity

Question

\cos(\theta)=\frac{8}{17}

0^\circ<\theta<90^\circ

\sec(\theta)

? Write your answer in simplified, rationalized form.

\sec(\theta)=

Posted 3 months ago

Question

\cos(x) = -0.3

\sin(90^\circ - x)

Posted 3 months ago

Question

\csc(\theta) = \frac{17}{8}

0^\circ < \theta < 90^\circ

\tan(\theta)

\newline

Write your answer in simplified, rationalized form.

\newline

\tan(\theta) =

\newline

Posted 3 months ago

Question

Is the sine function even or odd?

\newline

\newline

\text{[A]even}

\newline

\text{[B]odd}

Posted 3 months ago

Question

Write the sentence as an equation.

\newline

89

is equal to the quotient of

y

17

\newline

/

) if you want to use a division sign.

\newline

Posted 2 months ago

Question

Write the sentence as an equation.

\newline

45

is equal to the quotient of

z

5

\newline

/

) if you want to use a division sign.

\newline

Posted 4 months ago

Question

h

\newline

h^2 + 24h = 0

\newline

Write each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.

\newline

h =

Posted 4 months ago

Question

h^2 - 4h = 0

Posted 2 months ago

Question

Combine the like terms to create an equivalent expression:

\newline

-k-(-8k)=\square

Posted 4 months ago

Question

Which of the following degree measures is equal to

5 \pi

\newline

(The number of degrees of arc in a circle is

360

. The number of radians of arc in a circle is

2 \pi

\newline

1

\newline

144^{\circ}

\newline

900^{\circ}

\newline

1,080^{\circ}

\newline

1,800^{\circ}

Posted 2 months ago