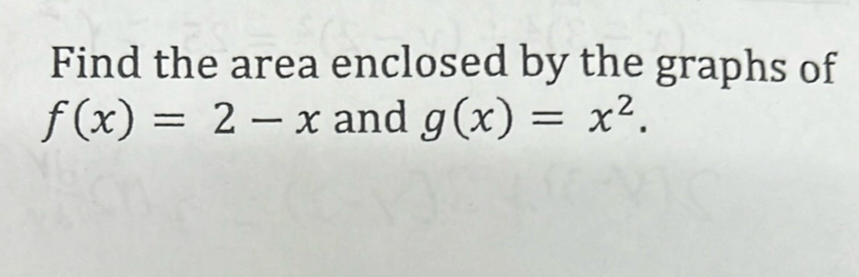Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the area enclosed by the graphs of
f(x)=2-x and
g(x)=x^(2)

Find the area enclosed by the graphs of $f(x)=2-x$ and $g(x)=x^{2}$

View step-by-step help

View step-by-step help

Domain and range of quadratic functions: equations

Full solution

Q. Find the area enclosed by the graphs of

f(x)=2-x

and

g(x)=x^{2}

Identify Intersection Points: Identify the points of intersection between $f(x) = 2 - x$ and $g(x) = x^2$ . Set $2 - x = x^2$ . $x^2 + x - 2 = 0$ . Factorize: $(x + 2)(x - 1) = 0$ . $x = -2$ , $x = 1$ .
Set Up Integral: Set up the integral to find the area between the curves from $x = -2$ to $x = 1$ . The area $A$ is given by the integral from $-2$ to $1$ of $(2 - x - x^2) \, dx$ .
Calculate Integral: Calculate the integral. $\newline$ $A = \int_{-2}^{1} (2 - x - x^2) dx.$ $\newline$ $= [2x - \frac{x^2}{2} - \frac{x^3}{3}] \text{ from } -2 \text{ to } 1.$ $\newline$ $= (2(1) - (1)^2/2 - (1)^3/3) - (2(-2) - (-2)^2/2 - (-2)^3/3).$ $\newline$ $= (2 - 1/2 - 1/3) - (-4 - 2 - (-8/3)).$ $\newline$ $= (3/2 - 1/3) - (-4 - 2 + 8/3).$ $\newline$ $= (9/6 - 2/6) - (-18/3 - 6/3 + 8/3).$ $\newline$ $= 7/6 - (-16/3).$ $\newline$ $= 7/6 + 16/3.$ $\newline$ $= 7/6 + 32/6.$ $\newline$ $= 39/6.$ $\newline$ $= [2x - \frac{x^2}{2} - \frac{x^3}{3}] \text{ from } -2 \text{ to } 1.$ $0$

More problems from Domain and range of quadratic functions: equations

Question

Solve by completing the square.

\newline

m^2 - 10m - 29 = 0

\newline

Write your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.

\newline

`m` = ____ or `m` = _____

Posted 1 month ago

Question

g(x)

g(x)

is the translation

5

f(x)=x^2

\newline

Write your answer in the form

a(x–h)^2+k

a

h

k

\newline

g(x)=

Posted 1 month ago

Question

What is the range of this quadratic function?

\newline

y = x^2 - 4x + 4

\newline

\newline

\left\{y \mid y \geq 2\right\}

\newline

\left\{y \mid y \leq 0\right\}

\newline

\left\{y \mid y \geq 0\right\}

\newline

\text{all real numbers}

Posted 1 month ago

Question

Write the equation of the parabola that passes through the points

(1,0)

(2,0)

(3,\text{–}16)

. Write your answer in the form

y = a(x – p)(x – q)

a

p

q

are integers, decimals, or simplified fractions.

\newline

Posted 1 month ago

Question

Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.

\newline

f^2 + 8f + \_\_\_\_\_

Posted 1 month ago

Question

h

\newline

h^2 + 39h = 0

\newline

\newline

Write each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.

\newline

h =

\newline

Posted 1 month ago

Question

Write a quadratic function with zeros

-9

-7

\newline

Write your answer using the variable

x

and in standard form with a leading coefficient of

1

\newline

f(x) = \_\_\_\_\_

Posted 2 months ago

Question

Find the equation of the axis of symmetry for the parabola

y = x^2

\newline

Simplify any numbers and write them as proper fractions, improper fractions, or integers.

\newline

\underline{\hspace{3cm}}

Posted 2 months ago

Question

g(x)

g(x)

is the translation

8

f(x) = x^2

\newline

Write your answer in the form

a(x – h)^2 + k

a

h

k

\newline

g(x) =

\newline

Posted 2 months ago

Question

x

\newline

x^2 = 1

\newline

\newline

Write your answer in simplified, rationalized form.

\newline

x =

x =

\newline

Posted 2 months ago