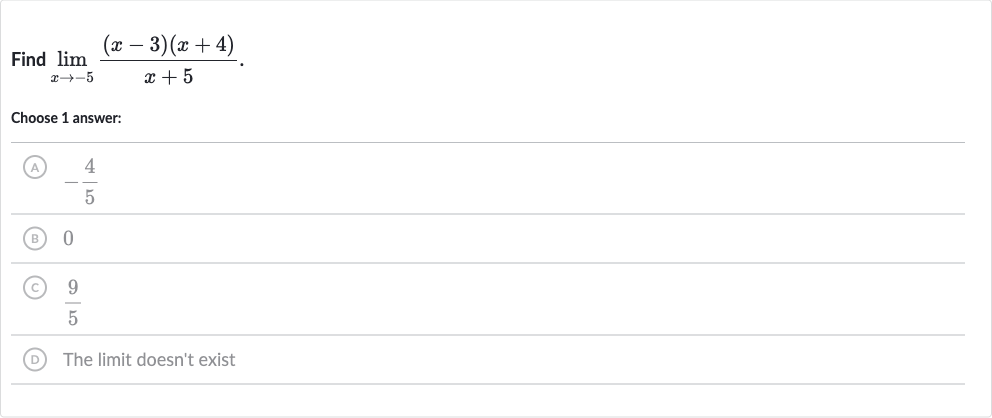
Find lim_(x rarr-5)((x-3)(x+4))/(x+5) Choose 1 answer: (A) -(4)/(5) (B) 0 (C) (9)/(5) (D) The limit doesn't exist

Question

Find  lim_(x rarr-5)((x-3)(x+4))/(x+5) Choose 1 answer: (A)  -(4)/(5) (B) 0 (C)  (9)/(5) (D) The limit doesn't exist

Bytelearn · Accepted Answer

Identify Form of Limit: Identify the form of the limit. We need to find the limit of the function (x-3)(x+4)/(x+5) as x approaches -5. Let's substitute x with -5 to see if the function is defined at that point. lim_(x -> -5) ((x-3)(x+4))/(x+5) = ((-5-3)(-5+4))/(-5+5)Check for Indeterminate Forms: Perform the substitution to check for indeterminate forms. Substituting -5 into the function gives us: ((-5-3)(-5+4))/(-5+5) = ((-8)(-1))/0 This results in a division by zero, which is undefined. However, since we are dealing with a limit, we need to check if the function approaches a specific value as x approaches -5.Simplify Expression: Simplify the expression to see if the limit can be determined. Since the denominator becomes 0 when x = -5, we have an indeterminate form of the type 0/0. This means we can apply algebraic manipulation to simplify the expression and possibly eliminate the indeterminate form.Factor Out Common Factor: Factor out the common factor in the numerator and denominator. Notice that the numerator (x-3)(x+4) can be rewritten as (x+5-8)(x+4), and we can see that (x+5) is a common factor in the numerator and denominator. However, since we are not actually factoring out (x+5) from the numerator, we realize that there is no common factor to cancel out with the denominator. This means we cannot simplify the expression by canceling out the (x+5) term.

Find $\lim _{x \rightarrow-5} \frac{(x-3)(x+4)}{x+5}$ $\newline$ Choose $1$ answer: $\newline$ (A) $-\frac{4}{5}$ $\newline$ (B) $0$ $\newline$ (C) $\frac{9}{5}$ $\newline$ (D) The limit doesn't exist

Full solution

More problems from Power rule

Related topics

Find lim⁡x→−5(x−3)(x+4)x+5 \lim _{x \rightarrow-5} \frac{(x-3)(x+4)}{x+5} limx→−5​x+5(x−3)(x+4)​\newlineChoose 111 answer:\newline(A) −45 -\frac{4}{5} −54​\newline(B) 000\newline(C) 95 \frac{9}{5} 59​\newline(D) The limit doesn't exist

Find $\lim _{x \rightarrow-5} \frac{(x-3)(x+4)}{x+5}$ $\newline$ Choose $1$ answer: $\newline$ (A) $-\frac{4}{5}$ $\newline$ (B) $0$ $\newline$ (C) $\frac{9}{5}$ $\newline$ (D) The limit doesn't exist