Full solution
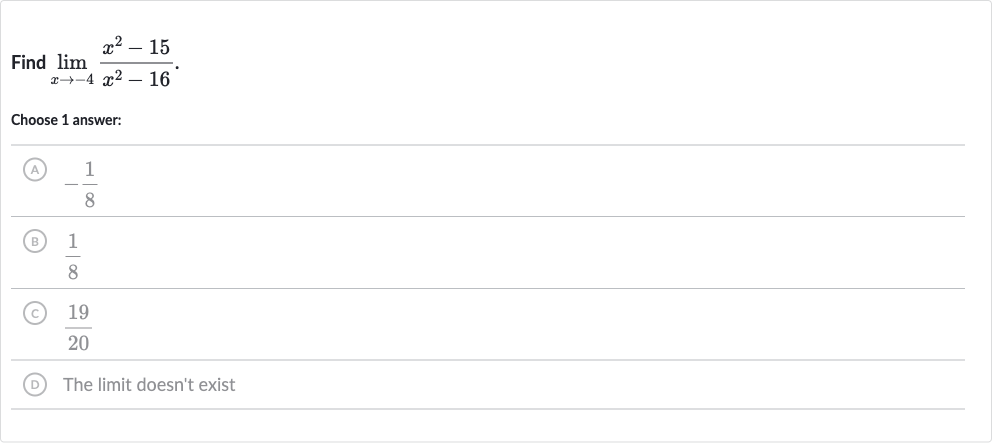
Q. Find .Choose answer:(A) (B) (C) (D) The limit doesn't exist
- Substitute : We are asked to find the limit of the function as approaches . Let's first try to directly substitute into the function to see if the limit can be computed this way.
- Calculate numerator and denominator: Substitute into the function:
- Factor the denominator: Calculate the numerator and the denominator separately:Numerator: Denominator:
- Rewrite the limit expression: We notice that the denominator becomes , which means the function is undefined at . However, this does not necessarily mean that the limit does not exist. We need to factor the denominator to see if there is a common factor that can be canceled out with the numerator.
- Conclusion: Factor the denominator: can be factored as .
- Conclusion: Factor the denominator: can be factored as .Now, let's rewrite the limit expression with the factored denominator:
- Conclusion: Factor the denominator: can be factored as .Now, let's rewrite the limit expression with the factored denominator:We see that there is no common factor between the numerator and the denominator that can be canceled out. Since the denominator is zero and the numerator is non-zero when , the limit does not exist.
More problems from Power rule
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help