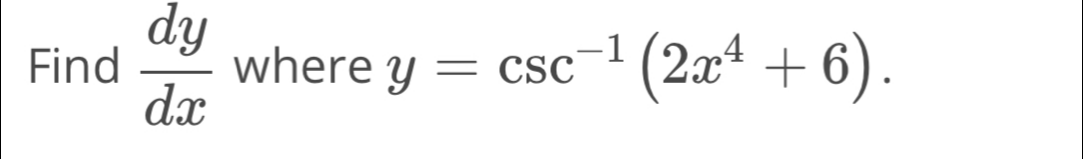Find (dy)/(dx) where y=csc^(-1)(2x^(4)+6).

Question

Find  (dy)/(dx) where  y=csc^(-1)(2x^(4)+6).

Bytelearn · Accepted Answer

Understand the function: Understand the function and what is being asked. We need to find the derivative of y with respect to x, where y = csc^(-1)(2x^4 + 6). This is an application of implicit differentiation and the chain rule.Differentiate both sides: Differentiate both sides of the equation with respect to x. Starting with y = csc^(-1)(2x^4 + 6), we differentiate both sides with respect to x. The left side becomes dy/dx, and the right side requires the use of the chain rule.Apply inverse cosecant derivative: Apply the derivative of the inverse cosecant function. The derivative of csc^(-1)(u) with respect to u is -1/(|u|sqrt(u^2 - 1)), where u is a function of x. In this case, u = 2x^4 + 6.Apply the chain rule: Apply the chain rule. Now we need to multiply the derivative of csc^(-1)(u) by the derivative of u with respect to x, which is d/dx(2x^4 + 6) = 8x^3.Combine to find dy/dx: Combine the results to find dy/dx. So, dy/dx = -1/(|2x^4 + 6|sqrt((2x^4 + 6)^2 - 1)) * 8x^3.Simplify the expression: Simplify the expression. Since 2x^4 + 6 is always positive for all real x, we can remove the absolute value. Also, we can expand the square and subtract 1 inside the square root. dy/dx = -8x^3 / ((2x^4 + 6)sqrt((2x^4 + 6)^2 - 1)).Further simplify if possible: Further simplify the expression if possible. The expression is already in its simplest form, so no further simplification is needed.

Find $\frac{d y}{d x}$ where $y=\csc ^{-1}\left(2 x^{4}+6\right)$ .

Full solution

More problems from Find trigonometric ratios using reference angles

Related topics

Find dydx \frac{d y}{d x} dxdy​ where y=csc⁡−1(2x4+6) y=\csc ^{-1}\left(2 x^{4}+6\right) y=csc−1(2x4+6).

Find $\frac{d y}{d x}$ where $y=\csc ^{-1}\left(2 x^{4}+6\right)$ .