AI tutor
Full solution
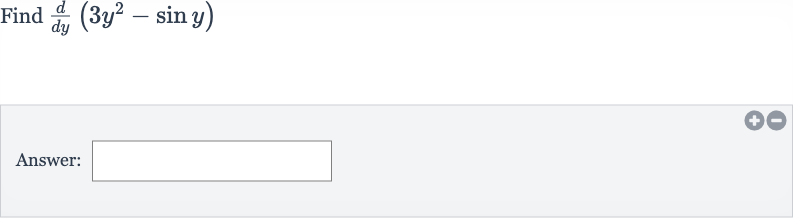
Q. Find Answer:
- Apply Differentiation Rules: To find the derivative of the function with respect to , we will apply the basic differentiation rules. The power rule for the term and the derivative of the sine function for the term .
- Differentiate : Differentiate with respect to . According to the power rule, the derivative of with respect to is . Therefore, the derivative of is .
- Differentiate : Differentiate with respect to . The derivative of with respect to is , so the derivative of is .
- Combine Derivatives: Combine the derivatives of the two terms to get the derivative of the entire function. The derivative of with respect to is .
More problems from Find trigonometric functions using a calculator
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help