AI tutor
Full solution
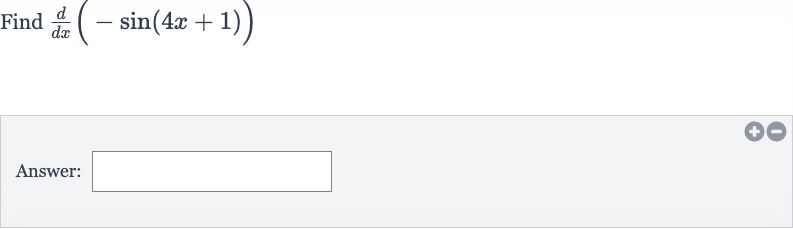
Q. Find Answer:
- Identify Functions: We are asked to find the derivative of the function with respect to . To do this, we will use the chain rule, which states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function.
- Derivative of Outer Function: First, let's identify the outer function and the inner function. The outer function is , and the inner function is . We will take the derivative of the outer function with respect to , and then multiply it by the derivative of the inner function with respect to .
- Derivative of Inner Function: The derivative of with respect to is , according to the derivative rule for sine, which states that . Since we have a negative sign in front of , it becomes .
- Apply Chain Rule: Now, we need to find the derivative of the inner function with respect to . The derivative of with respect to is , and the derivative of a constant ( in this case) is . So, the derivative of with respect to is .
- Simplify Final Answer: We can now apply the chain rule. The derivative of with respect to is the derivative of the outer function evaluated at the inner function times the derivative of the inner function . So, we have:
- Simplify Final Answer: We can now apply the chain rule. The derivative of with respect to is the derivative of the outer function evaluated at the inner function times the derivative of the inner function . So, we have: Simplify the expression to get the final answer. Multiplying by gives us:This is the derivative of with respect to .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help