AI tutor
Full solution
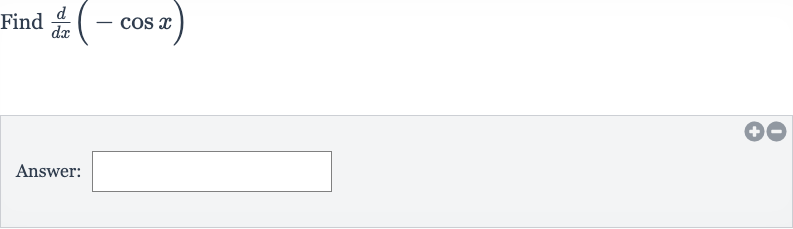
Q. Find Answer:
- Identify Function: We are asked to find the derivative of the function with respect to . The derivative of with respect to is , according to the basic differentiation rules. Since we have a negative sign in front of , we will apply the constant multiple rule which states that the derivative of a constant times a function is the constant times the derivative of the function.
- Apply Constant Multiple Rule: Applying the constant multiple rule, we differentiate by multiplying the derivative of with respect to by the constant .The derivative of is , so the derivative of is .
- Simplify Expression: Simplifying the expression, we get:.