Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find
(d)/(dx)(-4sin x)
Answer:

Find $\frac{d}{d x}(-4 \sin x)$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

Q. Find

\frac{d}{d x}(-4 \sin x)

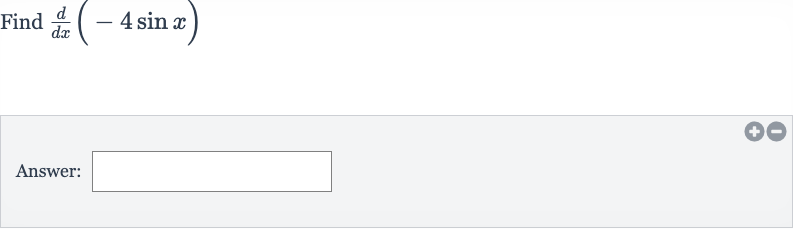
\newline

Answer:

Identify function: Identify the function to differentiate. $\newline$ We need to find the derivative of the function $f(x) = -4\sin(x)$ with respect to $x$ .
Apply sine rule: Apply the derivative rule for sine function. $\newline$ The derivative of $\sin(x)$ with respect to $x$ is $\cos(x)$ . Therefore, the derivative of $-4\sin(x)$ will be $-4$ times the derivative of $\sin(x)$ .
Calculate derivative: Calculate the derivative. $\newline$ Using the rule from Step $2$ , we get: $\newline$ $\frac{d}{dx}(-4\sin(x)) = -4 \cdot \frac{d}{dx}(\sin(x)) = -4 \cdot \cos(x)$
Write final answer: Write the final answer. $\newline$ The derivative of $-4\sin(x)$ with respect to $x$ is $-4\cos(x)$ .

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant