AI tutor
Full solution
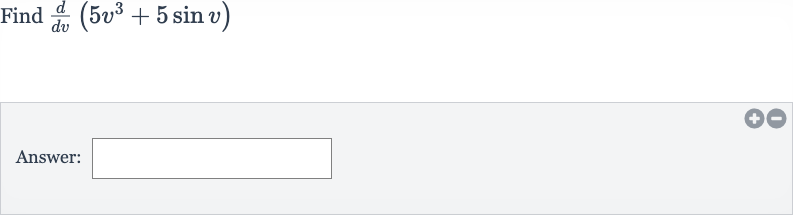
Q. Find Answer:
- Identify Function: Identify the function to differentiate.We are given the function , and we need to find its derivative with respect to .
- Apply Sum Rule: Apply the sum rule for differentiation.The sum rule states that the derivative of a sum of functions is the sum of their derivatives. Therefore, we can differentiate each term separately.
- Differentiate First Term: Differentiate the first term . Using the power rule, which states that the derivative of is , we differentiate to get .
- Differentiate Second Term: Differentiate the second term . The derivative of with respect to is , so the derivative of is .
- Combine Derivatives: Combine the derivatives of both terms.The derivative of the function is the sum of the derivatives of its terms, which we found in steps and . Therefore, the derivative is .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help