AI tutor
Full solution
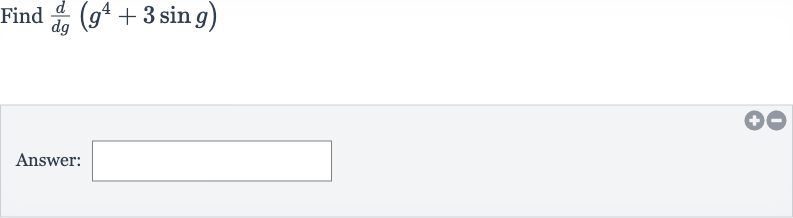
Q. Find Answer:
- Identify function: Identify the function to differentiate.We are given the function , and we need to find its derivative with respect to .
- Apply power rule: Apply the power rule to the first term.The power rule states that the derivative of with respect to is . Therefore, the derivative of with respect to is or .
- Apply sine rule: Apply the derivative rule for the sine function to the second term.The derivative of with respect to is . Therefore, the derivative of with respect to is .
- Combine derivatives: Combine the derivatives of both terms.The derivative of the function with respect to is the sum of the derivatives of its individual terms. So, we combine the results from Step and Step to get the final derivative.The derivative is .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help