AI tutor
Full solution
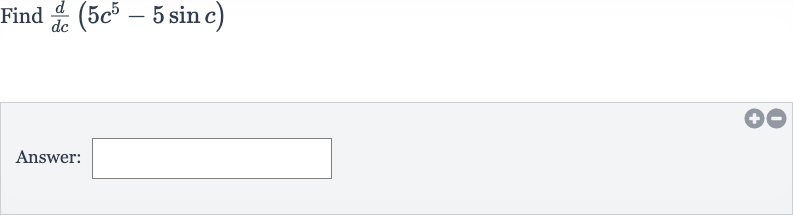
Q. Find Answer:
- Identify Common Factor: Identify the common factor in the numerator and denominator.The expression is . We can see that '' is a common factor in both the numerator and the denominator.
- Simplify Expression: Simplify the expression by canceling out the common factor.Since is present in both the numerator and the denominator, we can cancel it out. This gives us:
- Distribute Denominator: Distribute the denominator to both terms in the parenthesis.When we distribute to both terms in the parenthesis, we get:
- Further Simplify: Simplify the expression further if possible.In this case, there are no further simplifications that can be made, so the expression is already in its simplest form.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help