Full solution
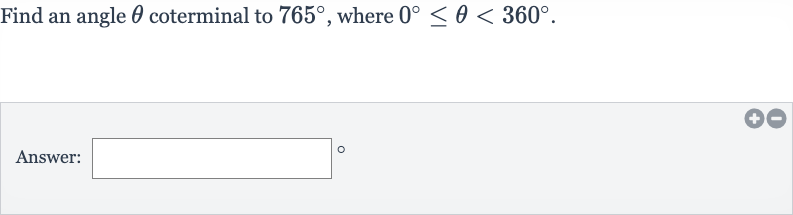
Q. Find an angle coterminal to , where .Answer:
- Subtract °: To find an angle coterminal to that lies between and , we need to subtract or add multiples of until the angle falls within the desired range. Since is greater than , we will subtract multiples of .Calculation:
- Subtract °: The result from the first step is still greater than , so we need to subtract once more.Calculation:
- Final Coterminal Angle: The result is now within the range of to , so we have found the coterminal angle.
More problems from Find trigonometric ratios using reference angles
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help