Full solution
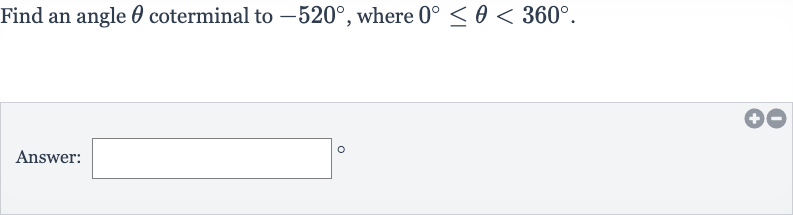
Q. Find an angle coterminal to , where .Answer:
- Add ° to °: To find a coterminal angle, we can add or subtract multiples of to the given angle until the result is within the desired range of to . Since is negative, we will add repeatedly until we get a positive angle in the correct range.
- Add ° to °: First addition: . The angle is still negative, so we need to add again.
- Final Coterminal Angle: Second addition: . This angle is positive and within the range of to , so it is a coterminal angle to .
More problems from Find trigonometric ratios using reference angles
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help