Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find an angle
theta coterminal to
-424^(@), where
0^(@) <= theta < 360^(@).
Answer:

Find an angle $\theta$ coterminal to $-424^{\circ}$ , where $0^{\circ} \leq \theta<360^{\circ}$ . $\newline$ Answer:

View step-by-step help

View step-by-step help

Find trigonometric ratios using a Pythagorean or reciprocal identity

Full solution

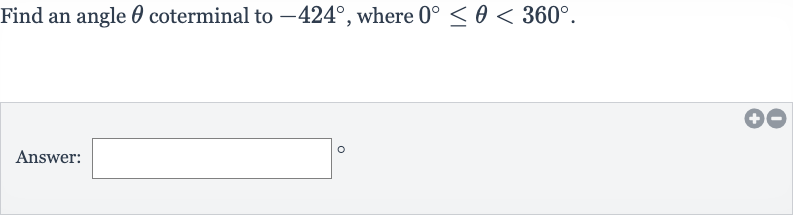
Q. Find an angle

\theta

coterminal to

-424^{\circ}

, where

0^{\circ} \leq \theta<360^{\circ}

.

\newline

Answer:

Add $360$ degrees: To find an angle coterminal to $-424$ degrees that is between $0$ and $360$ degrees, we need to add or subtract multiples of $360$ degrees until we get an angle in the desired range. Since $-424$ degrees is negative, we will add $360$ degrees until we are within the range of $0$ to $360$ degrees.
Add $360$ degrees: First, add $360$ degrees to $-424$ degrees to get a new angle. $\newline$ $-424$ degrees $+$ $360$ degrees $=$ $-64$ degrees $\newline$ This angle is still negative, so we need to add $360$ degrees again.
Check range: Add $360$ degrees to $-64$ degrees to get the coterminal angle. $\newline$ $-64$ degrees $+$ $360$ degrees $=$ $296$ degrees $\newline$ This angle is now within the desired range of $0$ to $360$ degrees.
Final coterminal angle: Check to ensure that $296$ degrees is indeed between $0$ and $360$ degrees. $\newline$ $0$ degrees $\leq$ $296$ degrees $<$ $360$ degrees $\newline$ This is true, so $296$ degrees is the coterminal angle we were looking for.

More problems from Find trigonometric ratios using a Pythagorean or reciprocal identity

Question

\cos(\theta)=\frac{8}{17}

0^\circ<\theta<90^\circ

\sec(\theta)

? Write your answer in simplified, rationalized form.

\sec(\theta)=

Posted 2 months ago

Question

\cos(x) = -0.3

\sin(90^\circ - x)

Posted 2 months ago

Question

\csc(\theta) = \frac{17}{8}

0^\circ < \theta < 90^\circ

\tan(\theta)

\newline

Write your answer in simplified, rationalized form.

\newline

\tan(\theta) =

\newline

Posted 2 months ago

Question

Is the sine function even or odd?

\newline

\newline

\text{[A]even}

\newline

\text{[B]odd}

Posted 2 months ago

Question

Write the sentence as an equation.

\newline

89

is equal to the quotient of

y

17

\newline

/

) if you want to use a division sign.

\newline

Posted 1 month ago

Question

Write the sentence as an equation.

\newline

45

is equal to the quotient of

z

5

\newline

/

) if you want to use a division sign.

\newline

Posted 3 months ago

Question

h

\newline

h^2 + 24h = 0

\newline

Write each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.

\newline

h =

Posted 3 months ago

Question

h^2 - 4h = 0

Posted 1 month ago

Question

Combine the like terms to create an equivalent expression:

\newline

-k-(-8k)=\square

Posted 4 months ago

Question

Which of the following degree measures is equal to

5 \pi

\newline

(The number of degrees of arc in a circle is

360

. The number of radians of arc in a circle is

2 \pi

\newline

1

\newline

144^{\circ}

\newline

900^{\circ}

\newline

1,080^{\circ}

\newline

1,800^{\circ}

Posted 1 month ago