Full solution
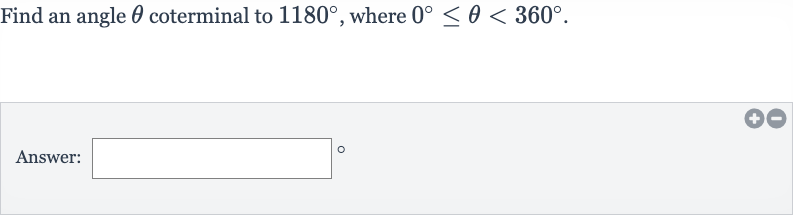
Q. Find an angle coterminal to , where .Answer:
- Understand coterminal angles: Understand what a coterminal angle is.Coterminal angles are angles that share the same initial and terminal sides but differ in the number of rotations. To find a coterminal angle within a specific range, we can add or subtract multiples of (a full rotation) from the given angle.
- Subtract multiples of °: Subtract multiples of from until the result is between and . (still greater than , so subtract another ) (still greater than , so subtract another ) (this is between and , so we have found our coterminal angle)
- Verify result in range: Verify that the result is within the specified range. is indeed between and , so it is a valid coterminal angle to .
More problems from Find trigonometric ratios using reference angles
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help