Full solution
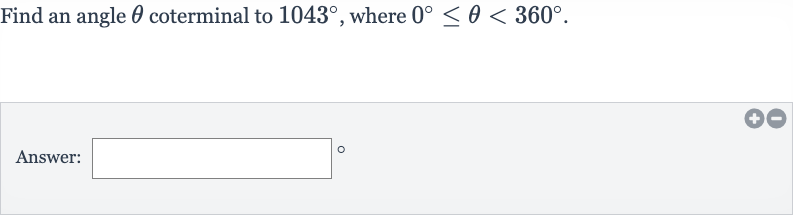
Q. Find an angle coterminal to , where .Answer:
- Divide by : To find an angle coterminal to that lies between and , we need to subtract or add multiples of until the angle is within the desired range.
- Subtract full rotations: First, we determine how many full rotations of are contained in . We do this by dividing by . This means that contains full rotations plus some extra degrees.
- Calculate coterminal angle: Since we are only interested in the extra degrees, we subtract the full rotations from .
- Calculate coterminal angle: Since we are only interested in the extra degrees, we subtract the full rotations from .The result, , is the coterminal angle to that lies between and .
More problems from Find trigonometric ratios using reference angles
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help