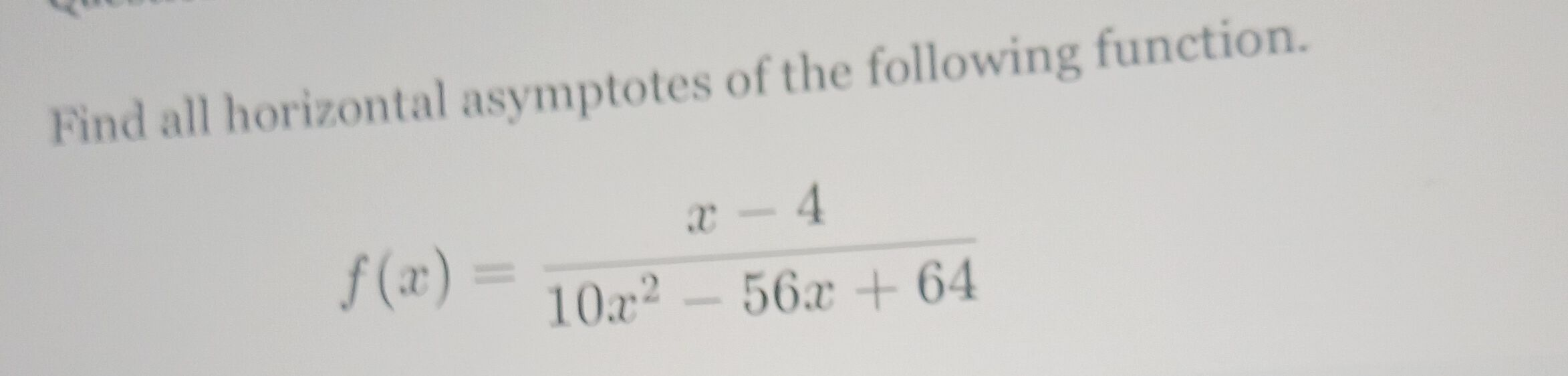Full solution
Q. Find all horizontal asymptotes of the following function.
- Understand Concept: Understand the concept of horizontal asymptotes for rational functions. Horizontal asymptotes occur where the function approaches a constant value as approaches infinity or negative infinity. For rational functions, horizontal asymptotes are determined by the degrees of the numerator and denominator polynomials.
- Compare Degrees: Compare the degrees of the numerator and the denominator.The degree of the numerator is , and the degree of the denominator is .
- Determine Asymptote: Determine the horizontal asymptote based on the degrees.Since the degree of the denominator is greater than the degree of the numerator, the horizontal asymptote is .
- Check Other Asymptotes: Check for any other possible horizontal asymptotes. There are no other possible horizontal asymptotes because the degree of the denominator is strictly greater than the degree of the numerator, which means the function will approach zero as approaches or .
More problems from Sin, cos, and tan of special angles
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help