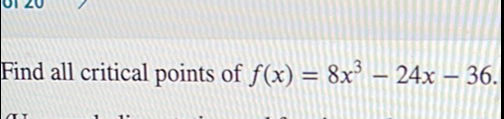Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find all critical points of
f(x)=8x^(3)-24 x-36.

Find all critical points of $f(x)=8 x^{3}-24 x-36$ .

View step-by-step help

View step-by-step help

Solve complex trigonomentric equations

Full solution

Q. Find all critical points of

f(x)=8 x^{3}-24 x-36

.

Calculate Derivative: To find the critical points of the function $f(x) = 8x^3 - 24x - 36$ , we need to find the values of $x$ where the first derivative $f'(x)$ is equal to zero or undefined.
Set Derivative Equal: First, we calculate the first derivative of $f(x)$ . The derivative of $8x^3$ is $24x^2$ , the derivative of $-24x$ is $-24$ , and the derivative of a constant $-36$ is $0$ . So, $f'(x) = 24x^2 - 24$ .
Simplify Equation: Next, we set the first derivative equal to zero to find the critical points: $24x^2 - 24 = 0$ .
Factorize Equation: We can simplify the equation by dividing both sides by $24$ , which gives us $x^2 - 1 = 0$ .
Find Solutions: The equation $x^2 - 1 = 0$ can be factored into $(x + 1)(x - 1) = 0$ .
Check Domain: Setting each factor equal to zero gives us two possible solutions for $x$ : $x + 1 = 0$ and $x - 1 = 0$ .
Check Domain: Setting each factor equal to zero gives us two possible solutions for $x$ : $x + 1 = 0$ and $x - 1 = 0$ .Solving $x + 1 = 0$ gives us $x = -1$ . Solving $x - 1 = 0$ gives us $x = 1$ . These are the $x$ -values where the first derivative is zero.
Check Domain: Setting each factor equal to zero gives us two possible solutions for $x$ : $x + 1 = 0$ and $x - 1 = 0$ .Solving $x + 1 = 0$ gives us $x = -1$ . Solving $x - 1 = 0$ gives us $x = 1$ . These are the $x$ -values where the first derivative is zero.We need to check if these points are within the domain of the original function $f(x)$ . Since $f(x)$ is a polynomial, its domain is all real numbers, so both $x = -1$ and $x = 1$ are within the domain.

More problems from Solve complex trigonomentric equations

Question

Find all solutions with

0^\circ \leq \theta \leq 180^\circ

. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.

\newline

\cos(\theta) = -1

\newline

\underline{\hspace{2em}}^\circ

Posted 7 months ago

Question

Kimi's school is

15

kilometers west of her house and

8

kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?

\newline

\_\_\_\_\_

Posted 7 months ago

Question

Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.

\newline

\cos 35^\circ =

Posted 7 months ago

Question

Find all solutions with

-90^\circ \leq \theta \leq 90^\circ

. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.

\newline

\csc(\theta) = -1

\newline

\_\_\_\_\,^\circ

Posted 8 months ago

Question

Evaluate. Write your answer in simplified, rationalized form. Do not round.

\newline

\cot 30^\circ =

Posted 7 months ago

Question

The terminal side of an angle

\theta

in standard position intersects the unit circle at

(\frac{84}{85}, \frac{13}{85})

\cos(\theta)

\newline

Write your answer in simplified, rationalized form.

\newline

Posted 7 months ago

Question

-90^\circ < \theta < 90^\circ

. Find the value of

\theta

\newline

\tan(\theta) = 0

\newline

Write your answer in simplified, rationalized form. Do not round.

\newline

\theta =

^\circ

\newline

Posted 8 months ago

Question

Evaluate. Write your answer in simplified, rationalized form. Do not round.

\newline

\csc 60^\circ =

Posted 8 months ago

Question

\theta

is an acute angle. Find the value of

\theta

\newline

\sec(\theta) = \sqrt{2}

\newline

\theta =

\degree

Posted 7 months ago

Question

Evaluate. Write your answer in simplified, rationalized form. Do not round.

\newline

\cos 90^\circ =

Posted 8 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant