Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find all angles, 0^(@) <= theta < 360^(@), that solve the following equation. tan theta=sqrt3 Answer: theta=

Find all angles, 0∘≤θ<360∘ 0^{\circ} \leq \theta<360^{\circ} , that solve the following equation.\newlinetan⁡θ=3 \tan \theta=\sqrt{3} \newlineAnswer: θ= \theta=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Find trigonometric ratios using reference anglesright chevron icon

Full solution

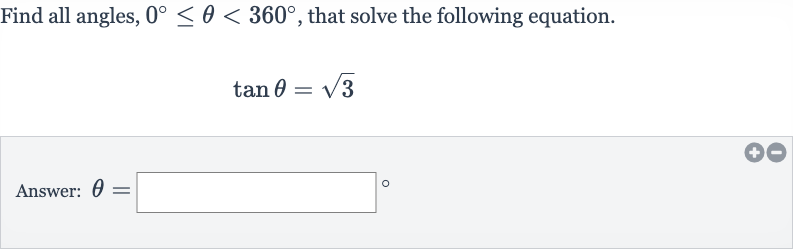
Q. Find all angles, 0∘≤θ<360∘ 0^{\circ} \leq \theta<360^{\circ} , that solve the following equation.\newlinetan⁡θ=3 \tan \theta=\sqrt{3} \newlineAnswer: θ= \theta=
  1. Recognize Equation: Recognize that the equation tan⁡(θ)=3\tan(\theta) = \sqrt{3} is looking for angles where the tangent function has the value of 3\sqrt{3}. The tangent function has the value of 3\sqrt{3} at angles where the opposite side over the adjacent side of a right triangle equals 3\sqrt{3}, which corresponds to an equilateral triangle cut in half, forming a 3030-6060-9090 triangle. Therefore, the reference angle for which tan⁡(θ)=3\tan(\theta) = \sqrt{3} is 6060 degrees.
  2. Find Reference Angle: Determine the angles in the interval [0,360)[0, 360) degrees where the tangent function is positive.\newlineTangent is positive in the first and third quadrants. Since the reference angle is 6060 degrees, the angles that satisfy the equation in these quadrants are 6060 degrees and 180+60=240180 + 60 = 240 degrees.
  3. Determine Positive Quadrants: Write down the final answer with the angles found in Step 22.\newlineThe angles that satisfy the equation tan⁡(θ)=3\tan(\theta) = \sqrt{3} in the interval [0,360)[0, 360) degrees are 6060 degrees and 240240 degrees.

More problems from Find trigonometric ratios using reference angles

Question
Find all solutions with 0∘≤θ≤180∘0^\circ \leq \theta \leq 180^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecos⁡(θ)=−1\cos(\theta) = -1\newline‾∘\underline{\hspace{2em}}^\circ
Get tutor helpright-arrow

Posted 1 month ago

Question
Kimi's school is 1515 kilometers west of her house and 88 kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?\newline_____\_\_\_\_\_ kilometers
Get tutor helpright-arrow

Posted 1 month ago

Question
Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.\newlinecos⁡35∘=\cos 35^\circ = __
Get tutor helpright-arrow

Posted 1 month ago

Question
Find all solutions with −90∘≤θ≤90∘-90^\circ \leq \theta \leq 90^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecsc⁡(θ)=−1\csc(\theta) = -1\newline____ ∘\_\_\_\_\,^\circ
Get tutor helpright-arrow

Posted 1 month ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecot⁡30∘=\cot 30^\circ = ______
Get tutor helpright-arrow

Posted 1 month ago

Question
The terminal side of an angle θ\theta in standard position intersects the unit circle at (8485,1385)(\frac{84}{85}, \frac{13}{85}). What is cos⁡(θ)\cos(\theta)?\newlineWrite your answer in simplified, rationalized form.\newline______
Get tutor helpright-arrow

Posted 1 month ago

Question
−90∘<θ<90∘-90^\circ < \theta < 90^\circ. Find the value of θ\theta in degrees.\newlinetan⁡(θ)=0\tan(\theta) = 0\newlineWrite your answer in simplified, rationalized form. Do not round.\newlineθ=\theta = ____∘^\circ\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecsc⁡60∘=\csc 60^\circ = ______
Get tutor helpright-arrow

Posted 1 month ago

Question
θ\theta is an acute angle. Find the value of θ\theta in degrees.\newlinesec⁡(θ)=2\sec(\theta) = \sqrt{2}\newlineθ=\theta = ____°\degree
Get tutor helpright-arrow

Posted 1 month ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecos⁡90∘=\cos 90^\circ = ____
Get tutor helpright-arrow

Posted 2 months ago

View all (102)