Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find all angles, 0^(@) <= theta < 360^(@), that satisfy the equation below, to the nearest tenth of a degree. 4sec^(2)theta-25=0 Answer: theta=

Find all angles, 0^{\circ} \leq \theta<360^{\circ} , that satisfy the equation below, to the nearest tenth of a degree.\newline4sec⁡2θ−25=0 4 \sec ^{2} \theta-25=0 \newlineAnswer: θ= \theta=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Csc, sec, and cot of special anglesright chevron icon

Full solution

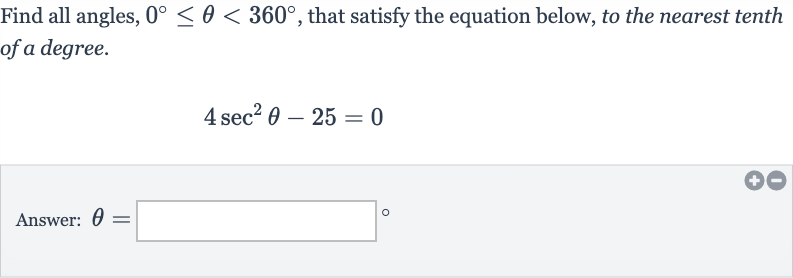
Q. Find all angles, 0∘≤θ<360∘ 0^{\circ} \leq \theta<360^{\circ} , that satisfy the equation below, to the nearest tenth of a degree.\newline4sec⁡2θ−25=0 4 \sec ^{2} \theta-25=0 \newlineAnswer: θ= \theta=
  1. Solve for sec⁡(θ)\sec(\theta): Solve the equation for sec⁡(θ)\sec(\theta).
    4sec⁡2(θ)−25=04\sec^2(\theta) - 25 = 0
    Add 2525 to both sides.
    4sec⁡2(θ)=254\sec^2(\theta) = 25
    Divide both sides by 44.
    sec⁡2(θ)=254\sec^2(\theta) = \frac{25}{4}
    Take the square root of both sides.
    sec⁡(θ)=±254\sec(\theta) = \pm\sqrt{\frac{25}{4}}
    sec⁡(θ)=±52\sec(\theta) = \pm\frac{5}{2}
  2. Find cosine values: Find the corresponding cosine values since sec⁡(θ)\sec(\theta) is the reciprocal of cos⁡(θ)\cos(\theta).sec⁡(θ)=1cos⁡(θ)\sec(\theta) = \frac{1}{\cos(\theta)}cos⁡(θ)=1sec⁡(θ)\cos(\theta) = \frac{1}{\sec(\theta)}cos⁡(θ)=±25\cos(\theta) = \pm\frac{2}{5}
  3. Determine cosine quadrants: Determine the quadrants where cosine is positive and negative.\newlineCosine is positive in the first and fourth quadrants and negative in the second and third quadrants.
  4. Principal angle for positive cosine: Use the inverse cosine function to find the principal angle for the positive cosine value. \newlineθ=cos⁡−1(25)\theta = \cos^{-1}(\frac{2}{5})\newlineCalculate the principal angle.\newlineθ≈cos⁡−1(0.4)\theta \approx \cos^{-1}(0.4)\newlineθ≈66.4∘\theta \approx 66.4^\circ
  5. Second angle for positive cosine: Find the second angle in the first cycle (0∘0^\circ to 360∘360^\circ) where cosine is positive.\newlineSince cosine is also positive in the fourth quadrant, the second angle is 360∘−66.4∘360^\circ - 66.4^\circ.\newlineθ≈360∘−66.4∘\theta \approx 360^\circ - 66.4^\circ\newlineθ≈293.6∘\theta \approx 293.6^\circ
  6. Principal angle for negative cosine: Use the inverse cosine function to find the principal angle for the negative cosine value.\newlineθ=cos⁡−1(−25)\theta = \cos^{-1}(-\frac{2}{5})\newlineCalculate the principal angle.\newlineθ≈cos⁡−1(−0.4)\theta \approx \cos^{-1}(-0.4)\newlineθ≈113.6∘\theta \approx 113.6^\circ
  7. Second angle for negative cosine: Find the second angle in the first cycle (0∘0^\circ to 360∘360^\circ) where cosine is negative.\newlineSince cosine is also negative in the third quadrant, the second angle is 180∘+(180∘−113.6∘)180^\circ + (180^\circ - 113.6^\circ).\newlineθ≈180∘+(180∘−113.6∘)\theta \approx 180^\circ + (180^\circ - 113.6^\circ)\newlineθ≈180∘+66.4∘\theta \approx 180^\circ + 66.4^\circ\newlineθ≈246.4∘\theta \approx 246.4^\circ

More problems from Csc, sec, and cot of special angles

Question
Find all solutions with 0∘≤θ≤180∘0^\circ \leq \theta \leq 180^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecos⁡(θ)=−1\cos(\theta) = -1\newline‾∘\underline{\hspace{2em}}^\circ
Get tutor helpright-arrow

Posted 7 months ago

Question
Kimi's school is 1515 kilometers west of her house and 88 kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?\newline_____\_\_\_\_\_ kilometers
Get tutor helpright-arrow

Posted 7 months ago

Question
Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.\newlinecos⁡35∘=\cos 35^\circ = __
Get tutor helpright-arrow

Posted 7 months ago

Question
Find all solutions with −90∘≤θ≤90∘-90^\circ \leq \theta \leq 90^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecsc⁡(θ)=−1\csc(\theta) = -1\newline____ ∘\_\_\_\_\,^\circ
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecot⁡30∘=\cot 30^\circ = ______
Get tutor helpright-arrow

Posted 7 months ago

Question
The terminal side of an angle θ\theta in standard position intersects the unit circle at (8485,1385)(\frac{84}{85}, \frac{13}{85}). What is cos⁡(θ)\cos(\theta)?\newlineWrite your answer in simplified, rationalized form.\newline______
Get tutor helpright-arrow

Posted 7 months ago

Question
−90∘<θ<90∘-90^\circ < \theta < 90^\circ. Find the value of θ\theta in degrees.\newlinetan⁡(θ)=0\tan(\theta) = 0\newlineWrite your answer in simplified, rationalized form. Do not round.\newlineθ=\theta = ____∘^\circ\newline
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecsc⁡60∘=\csc 60^\circ = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
θ\theta is an acute angle. Find the value of θ\theta in degrees.\newlinesec⁡(θ)=2\sec(\theta) = \sqrt{2}\newlineθ=\theta = ____°\degree
Get tutor helpright-arrow

Posted 7 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecos⁡90∘=\cos 90^\circ = ____
Get tutor helpright-arrow

Posted 8 months ago

View all (150)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant