Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find all angles, 0^(@) <= theta < 360^(@), that satisfy the equation below, to the nearest tenth of a degree. csc^(2)theta+5csc theta-6=0 Answer: theta=

Find all angles, 0^{\circ} \leq \theta<360^{\circ} , that satisfy the equation below, to the nearest tenth of a degree.\newlinecsc⁡2θ+5csc⁡θ−6=0 \csc ^{2} \theta+5 \csc \theta-6=0 \newlineAnswer: θ= \theta=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Csc, sec, and cot of special anglesright chevron icon

Full solution

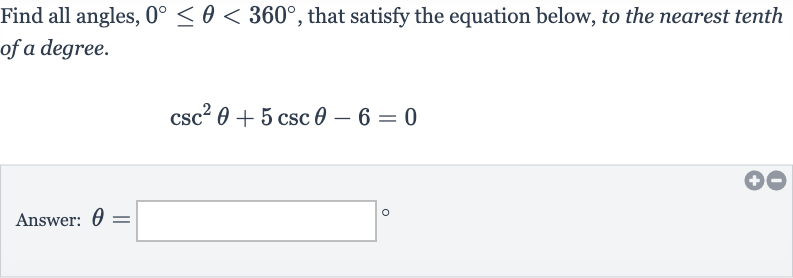
Q. Find all angles, 0∘≤θ<360∘ 0^{\circ} \leq \theta<360^{\circ} , that satisfy the equation below, to the nearest tenth of a degree.\newlinecsc⁡2θ+5csc⁡θ−6=0 \csc ^{2} \theta+5 \csc \theta-6=0 \newlineAnswer: θ= \theta=
  1. Set xx as csc⁡(θ)\csc(\theta): Recognize that the given equation is a quadratic equation in terms of csc⁡(θ)\csc(\theta). Let's set x=csc⁡(θ)x = \csc(\theta) to make it look more familiar.\newlineThe equation becomes x2+5x−6=0x^2 + 5x - 6 = 0.
  2. Factor the quadratic: Factor the quadratic equation. \newline(x+6)(x−1)=0(x + 6)(x - 1) = 0
  3. Solve for x: Solve for x.\newlinex+6=0x + 6 = 0 or x−1=0x - 1 = 0\newlinex=−6x = -6 or x=1x = 1
  4. Translate to csc⁡(θ)\csc(\theta): Translate the solutions for xx back into terms of csc⁡(θ)\csc(\theta).\newlinecsc⁡(θ)=−6\csc(\theta) = -6 or csc⁡(θ)=1\csc(\theta) = 1
  5. Use sine definition: Solve for θ\theta using the definition of cosecant, which is the reciprocal of sine.\newlineFor csc⁡(θ)=1\csc(\theta) = 1, sin⁡(θ)=1csc⁡(θ)=11=1\sin(\theta) = \frac{1}{\csc(\theta)} = \frac{1}{1} = 1.\newlineFor csc⁡(θ)=−6\csc(\theta) = -6, sin⁡(θ)=1csc⁡(θ)=1−6\sin(\theta) = \frac{1}{\csc(\theta)} = \frac{1}{-6}.
  6. Find sin⁡(θ)=1\sin(\theta) = 1: Find the angles that correspond to sin⁡(θ)=1\sin(\theta) = 1.\newlinesin⁡(θ)=1\sin(\theta) = 1 at θ=90°\theta = 90°.
  7. Find sin⁡(θ)=−16\sin(\theta) = -\frac{1}{6}: Find the angles that correspond to sin⁡(θ)=1−6\sin(\theta) = \frac{1}{-6}.\newlineSince the range of the sine function is [−1,1][-1, 1], and −16-\frac{1}{6} is within this range, we look for angles where the sine is negative. This occurs in the third and fourth quadrants.
  8. Find reference angle: Use the inverse sine function to find the reference angle for sin⁡(θ)=−16\sin(\theta) = -\frac{1}{6}.θref=arcsin⁡(16)≈9.6∘\theta_{\text{ref}} = \arcsin(\frac{1}{6}) \approx 9.6^\circ
  9. Determine angles: Determine the angles in the third and fourth quadrants that have this reference angle.\newlineFor the third quadrant: θ=180°+θref≈180°+9.6°≈189.6°\theta = 180° + \theta_{\text{ref}} \approx 180° + 9.6° \approx 189.6°\newlineFor the fourth quadrant: θ=360°−θref≈360°−9.6°≈350.4°\theta = 360° - \theta_{\text{ref}} \approx 360° - 9.6° \approx 350.4°
  10. Combine solutions: Combine all the solutions. θ=90°,189.6°,350.4°\theta = 90°, 189.6°, 350.4°

More problems from Csc, sec, and cot of special angles

Question
Find all solutions with 0∘≤θ≤180∘0^\circ \leq \theta \leq 180^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecos⁡(θ)=−1\cos(\theta) = -1\newline‾∘\underline{\hspace{2em}}^\circ
Get tutor helpright-arrow

Posted 7 months ago

Question
Kimi's school is 1515 kilometers west of her house and 88 kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?\newline_____\_\_\_\_\_ kilometers
Get tutor helpright-arrow

Posted 7 months ago

Question
Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.\newlinecos⁡35∘=\cos 35^\circ = __
Get tutor helpright-arrow

Posted 7 months ago

Question
Find all solutions with −90∘≤θ≤90∘-90^\circ \leq \theta \leq 90^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecsc⁡(θ)=−1\csc(\theta) = -1\newline____ ∘\_\_\_\_\,^\circ
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecot⁡30∘=\cot 30^\circ = ______
Get tutor helpright-arrow

Posted 7 months ago

Question
The terminal side of an angle θ\theta in standard position intersects the unit circle at (8485,1385)(\frac{84}{85}, \frac{13}{85}). What is cos⁡(θ)\cos(\theta)?\newlineWrite your answer in simplified, rationalized form.\newline______
Get tutor helpright-arrow

Posted 7 months ago

Question
−90∘<θ<90∘-90^\circ < \theta < 90^\circ. Find the value of θ\theta in degrees.\newlinetan⁡(θ)=0\tan(\theta) = 0\newlineWrite your answer in simplified, rationalized form. Do not round.\newlineθ=\theta = ____∘^\circ\newline
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecsc⁡60∘=\csc 60^\circ = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
θ\theta is an acute angle. Find the value of θ\theta in degrees.\newlinesec⁡(θ)=2\sec(\theta) = \sqrt{2}\newlineθ=\theta = ____°\degree
Get tutor helpright-arrow

Posted 7 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecos⁡90∘=\cos 90^\circ = ____
Get tutor helpright-arrow

Posted 9 months ago

View all (150)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant