Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find all angles, 0^(@) <= theta < 360^(@), that satisfy the equation below, to the nearest tenth of a degree. sin^(2)theta-sin theta=0 Answer: theta=

Find all angles, 0^{\circ} \leq \theta<360^{\circ} , that satisfy the equation below, to the nearest tenth of a degree.\newlinesin⁡2θ−sin⁡θ=0 \sin ^{2} \theta-\sin \theta=0 \newlineAnswer: θ= \theta=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Csc, sec, and cot of special anglesright chevron icon

Full solution

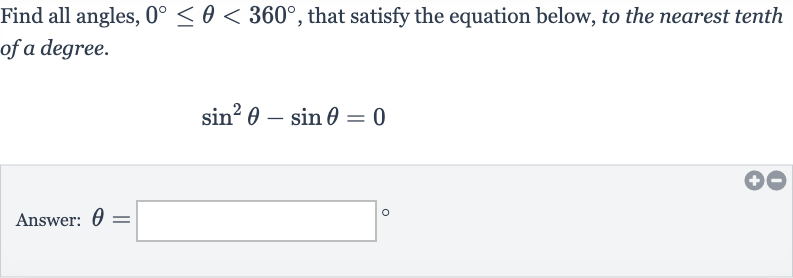
Q. Find all angles, 0∘≤θ<360∘ 0^{\circ} \leq \theta<360^{\circ} , that satisfy the equation below, to the nearest tenth of a degree.\newlinesin⁡2θ−sin⁡θ=0 \sin ^{2} \theta-\sin \theta=0 \newlineAnswer: θ= \theta=
  1. Factor Trigonometric Equation: Factor the given trigonometric equation. sin⁡2(θ)−sin⁡(θ)=0\sin^2(\theta) - \sin(\theta) = 0 can be factored as sin⁡(θ)⋅(sin⁡(θ)−1)=0\sin(\theta) \cdot (\sin(\theta) - 1) = 0.
  2. Set Factors Equal: Set each factor equal to zero to find the solutions for θ\theta.sin⁡(θ)=0\sin(\theta) = 0 and sin⁡(θ)−1=0\sin(\theta) - 1 = 0.
  3. Solve for Theta: Solve the first equation sin⁡(θ)=0\sin(\theta) = 0. The sine function is zero at 00 degrees, 180180 degrees, and 360360 degrees.
  4. Find Solutions: Solve the second equation sin⁡(θ)−1=0\sin(\theta) - 1 = 0. This simplifies to sin⁡(θ)=1\sin(\theta) = 1, which occurs at 9090 degrees.
  5. Compile All Solutions: Compile all the solutions.\newlineThe angles that satisfy the equation are 00 degrees, 9090 degrees, 180180 degrees, and 360360 degrees.

More problems from Csc, sec, and cot of special angles

Question
Find all solutions with 0∘≤θ≤180∘0^\circ \leq \theta \leq 180^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecos⁡(θ)=−1\cos(\theta) = -1\newline‾∘\underline{\hspace{2em}}^\circ
Get tutor helpright-arrow

Posted 7 months ago

Question
Kimi's school is 1515 kilometers west of her house and 88 kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?\newline_____\_\_\_\_\_ kilometers
Get tutor helpright-arrow

Posted 7 months ago

Question
Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.\newlinecos⁡35∘=\cos 35^\circ = __
Get tutor helpright-arrow

Posted 7 months ago

Question
Find all solutions with −90∘≤θ≤90∘-90^\circ \leq \theta \leq 90^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecsc⁡(θ)=−1\csc(\theta) = -1\newline____ ∘\_\_\_\_\,^\circ
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecot⁡30∘=\cot 30^\circ = ______
Get tutor helpright-arrow

Posted 7 months ago

Question
The terminal side of an angle θ\theta in standard position intersects the unit circle at (8485,1385)(\frac{84}{85}, \frac{13}{85}). What is cos⁡(θ)\cos(\theta)?\newlineWrite your answer in simplified, rationalized form.\newline______
Get tutor helpright-arrow

Posted 7 months ago

Question
−90∘<θ<90∘-90^\circ < \theta < 90^\circ. Find the value of θ\theta in degrees.\newlinetan⁡(θ)=0\tan(\theta) = 0\newlineWrite your answer in simplified, rationalized form. Do not round.\newlineθ=\theta = ____∘^\circ\newline
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecsc⁡60∘=\csc 60^\circ = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
θ\theta is an acute angle. Find the value of θ\theta in degrees.\newlinesec⁡(θ)=2\sec(\theta) = \sqrt{2}\newlineθ=\theta = ____°\degree
Get tutor helpright-arrow

Posted 7 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecos⁡90∘=\cos 90^\circ = ____
Get tutor helpright-arrow

Posted 9 months ago

View all (150)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant