Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find all angles, 0^(@) <= theta < 360^(@), that satisfy the equation below, to the nearest tenth of a degree. 16cot^(2)theta-1=0 Answer: theta=

Find all angles, 0∘≤θ<360∘ 0^{\circ} \leq \theta<360^{\circ} , that satisfy the equation below, to the nearest tenth of a degree.\newline16cot⁡2θ−1=0 16 \cot ^{2} \theta-1=0 \newlineAnswer: θ= \theta=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Evaluate variable expressions for number sequencesright chevron icon

Full solution

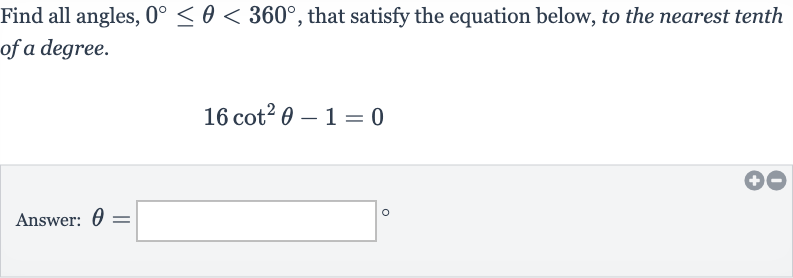
Q. Find all angles, 0∘≤θ<360∘ 0^{\circ} \leq \theta<360^{\circ} , that satisfy the equation below, to the nearest tenth of a degree.\newline16cot⁡2θ−1=0 16 \cot ^{2} \theta-1=0 \newlineAnswer: θ= \theta=
  1. Solve for cot⁡2(θ)\cot^2(\theta): Solve the equation for cot⁡2(θ)\cot^2(\theta).
    16cot⁡2(θ)−1=016\cot^2(\theta) - 1 = 0
    Add 11 to both sides of the equation.
    16cot⁡2(θ)=116\cot^2(\theta) = 1
    Divide both sides by 1616.
    cot⁡2(θ)=116\cot^2(\theta) = \frac{1}{16}
    Take the square root of both sides.
    cot⁡(θ)=±14\cot(\theta) = \pm\frac{1}{4}
  2. Find positive cotangent angles: Find the angles that correspond to the positive cotangent value.\newlinecot⁡(θ)=14\cot(\theta) = \frac{1}{4}\newlineSince cotangent is the reciprocal of tangent, we have:\newlinetan⁡(θ)=4\tan(\theta) = 4\newlineUse the arctangent function to find the angle whose tangent is 44.\newlineθ=arctan⁡(4)\theta = \arctan(4)\newlineUse a calculator to find the value of θ\theta.\newlineθ≈75.96\theta \approx 75.96 degrees\newlineHowever, cotangent is positive in the first and third quadrants, so we need to find the angle in the third quadrant as well.\newlineθ=180+75.96\theta = 180 + 75.96\newlineθ≈255.96\theta \approx 255.96 degrees
  3. Find negative cotangent angles: Find the angles that correspond to the negative cotangent value.\newlinecot⁡(θ)=−14\cot(\theta) = -\frac{1}{4}\newlineSince cotangent is the reciprocal of tangent, we have:\newlinetan⁡(θ)=−4\tan(\theta) = -4\newlineUse the arctangent function to find the angle whose tangent is −4-4.\newlineθ=arctan⁡(−4)\theta = \arctan(-4)\newlineUse a calculator to find the value of θ\theta.\newlineθ≈−75.96\theta \approx -75.96 degrees\newlineHowever, we need angles between 00 and 360360 degrees, so we add 180180 degrees to find the angle in the second quadrant.\newlineθ=180−75.96\theta = 180 - 75.96\newlineθ≈104.04\theta \approx 104.04 degrees\newlineAnd add 360360 degrees to find the angle in the fourth quadrant.\newlinetan⁡(θ)=−4\tan(\theta) = -411\newlinetan⁡(θ)=−4\tan(\theta) = -422 degrees
  4. List all satisfying angles: List all the angles that satisfy the equation.\newlineWe have found four angles that satisfy the equation:\newlineθ≈75.96\theta \approx 75.96 degrees (first quadrant)\newlineθ≈255.96\theta \approx 255.96 degrees (third quadrant)\newlineθ≈104.04\theta \approx 104.04 degrees (second quadrant)\newlineθ≈284.04\theta \approx 284.04 degrees (fourth quadrant)\newlineRound each angle to the nearest tenth of a degree.\newlineθ≈76.0\theta \approx 76.0 degrees\newlineθ≈256.0\theta \approx 256.0 degrees\newlineθ≈104.0\theta \approx 104.0 degrees\newlineθ≈284.0\theta \approx 284.0 degrees

More problems from Evaluate variable expressions for number sequences

Question
Find the sum of the finite arithmetic series. ∑n=110(7n+4)\sum_{n=1}^{10} (7n+4)\newline______
Get tutor helpright-arrow

Posted 3 months ago

Question
Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`
Get tutor helpright-arrow

Posted 2 months ago

Question
Type the missing number in this sequence: `2, 4 8`, ______,`32`
Get tutor helpright-arrow

Posted 2 months ago

Question
What kind of sequence is this? 2,10,50,250,…2, 10, 50, 250, \ldots Choices:Choices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the missing number in this pattern? 1,4,9,16,25,36,49,64,81,____1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_
Get tutor helpright-arrow

Posted 2 months ago

Question
Classify the series. ∑n=012(n+2)3 \sum_{n = 0}^{12} (n + 2)^3 \newlineChoices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the first three partial sums of the series.\newline1+6+11+16+21+26+⋯1 + 6 + 11 + 16 + 21 + 26 + \cdots\newlineWrite your answers as integers or fractions in simplest form.\newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the third partial sum of the series. \newline3+9+15+21+27+33+⋯3 + 9 + 15 + 21 + 27 + 33 + \cdots\newlineWrite your answer as an integer or a fraction in simplest form. \newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the first three partial sums of the series. \newline1+7+13+19+25+31+⋯1 + 7 + 13 + 19 + 25 + 31 + \cdots\newlineWrite your answers as integers or fractions in simplest form. \newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 3 months ago

Question
Does the infinite geometric series converge or diverge?\newline1+34+916+2764+⋯1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots\newlineChoices:\newline[A]converge\text{[A]converge}\newline[B]diverge\text{[B]diverge}
Get tutor helpright-arrow

Posted 2 months ago

View all (74)