Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find all angles, 0^(@) <= theta < 360^(@), that satisfy the equation below, to the nearest tenth of a degree. 9cot^(2)theta-1=0 Answer: theta=

Find all angles, 0∘≤θ<360∘ 0^{\circ} \leq \theta<360^{\circ} , that satisfy the equation below, to the nearest tenth of a degree.\newline9cot⁡2θ−1=0 9 \cot ^{2} \theta-1=0 \newlineAnswer: θ= \theta=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Csc, sec, and cot of special anglesright chevron icon

Full solution

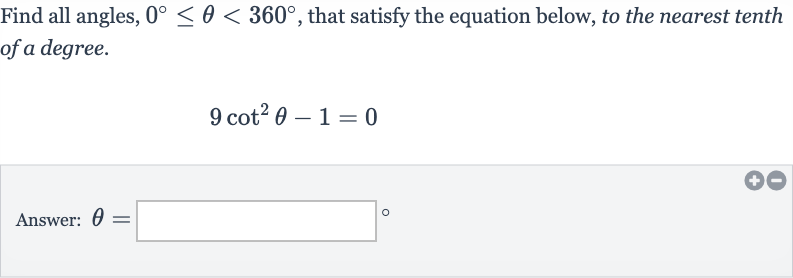
Q. Find all angles, 0∘≤θ<360∘ 0^{\circ} \leq \theta<360^{\circ} , that satisfy the equation below, to the nearest tenth of a degree.\newline9cot⁡2θ−1=0 9 \cot ^{2} \theta-1=0 \newlineAnswer: θ= \theta=
  1. Solve for cotangent: Solve the equation for cot⁡2(θ)\cot^2(\theta). \newline9cot⁡2(θ)−1=09\cot^2(\theta) - 1 = 0\newlineAdd 11 to both sides of the equation.\newline9cot⁡2(θ)=19\cot^2(\theta) = 1\newlineDivide both sides by 99.\newlinecot⁡2(θ)=19\cot^2(\theta) = \frac{1}{9}\newlineTake the square root of both sides.\newlinecot⁡(θ)=±13\cot(\theta) = \pm\frac{1}{3}
  2. Find corresponding angles: Find the angles that correspond to the cotangent values.\newlineSince cotangent is the reciprocal of tangent, we can write:\newlinetan⁡(θ)=±3\tan(\theta) = \pm 3
  3. Positive tangent value: Determine the angles for the positive tangent value.\newlineUsing a calculator or trigonometric tables, find the angle whose tangent is 33.\newlinetan⁡−1(3)≈71.6∘\tan^{-1}(3) \approx 71.6^\circ\newlineSince tangent is positive in the first and third quadrants, we add 180∘180^\circ to find the angle in the third quadrant.\newline71.6∘+180∘=251.6∘71.6^\circ + 180^\circ = 251.6^\circ
  4. Negative tangent value: Determine the angles for the negative tangent value.\newlineSince tangent is negative in the second and fourth quadrants, we find the reference angle for tan⁡−1(−3)\tan^{-1}(-3).\newlinetan⁡−1(−3)≈−71.6∘\tan^{-1}(-3) \approx -71.6^\circ\newlineTo find the angle in the second quadrant, we add 180∘180^\circ to the reference angle.\newline180∘−71.6∘=108.4∘180^\circ - 71.6^\circ = 108.4^\circ\newlineTo find the angle in the fourth quadrant, we add 360∘360^\circ to the reference angle.\newline360∘−71.6∘=288.4∘360^\circ - 71.6^\circ = 288.4^\circ
  5. List of satisfying angles: List all the angles that satisfy the original equation. θ≈71.6∘,108.4∘,251.6∘,288.4∘\theta \approx 71.6^\circ, 108.4^\circ, 251.6^\circ, 288.4^\circ

More problems from Csc, sec, and cot of special angles

Question
Find all solutions with 0∘≤θ≤180∘0^\circ \leq \theta \leq 180^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecos⁡(θ)=−1\cos(\theta) = -1\newline‾∘\underline{\hspace{2em}}^\circ
Get tutor helpright-arrow

Posted 2 months ago

Question
Kimi's school is 1515 kilometers west of her house and 88 kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?\newline_____\_\_\_\_\_ kilometers
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.\newlinecos⁡35∘=\cos 35^\circ = __
Get tutor helpright-arrow

Posted 2 months ago

Question
Find all solutions with −90∘≤θ≤90∘-90^\circ \leq \theta \leq 90^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecsc⁡(θ)=−1\csc(\theta) = -1\newline____ ∘\_\_\_\_\,^\circ
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecot⁡30∘=\cot 30^\circ = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
The terminal side of an angle θ\theta in standard position intersects the unit circle at (8485,1385)(\frac{84}{85}, \frac{13}{85}). What is cos⁡(θ)\cos(\theta)?\newlineWrite your answer in simplified, rationalized form.\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
−90∘<θ<90∘-90^\circ < \theta < 90^\circ. Find the value of θ\theta in degrees.\newlinetan⁡(θ)=0\tan(\theta) = 0\newlineWrite your answer in simplified, rationalized form. Do not round.\newlineθ=\theta = ____∘^\circ\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecsc⁡60∘=\csc 60^\circ = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
θ\theta is an acute angle. Find the value of θ\theta in degrees.\newlinesec⁡(θ)=2\sec(\theta) = \sqrt{2}\newlineθ=\theta = ____°\degree
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecos⁡90∘=\cos 90^\circ = ____
Get tutor helpright-arrow

Posted 3 months ago

View all (206)