Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find a formula for the inverse of the following function, if possible.
G(x)=root(5)(4x+2)

Find a formula for the inverse of the following function, if possible. $\newline$ $G(x)=\sqrt[5]{4 x+2}$

View step-by-step help

View step-by-step help

Full solution

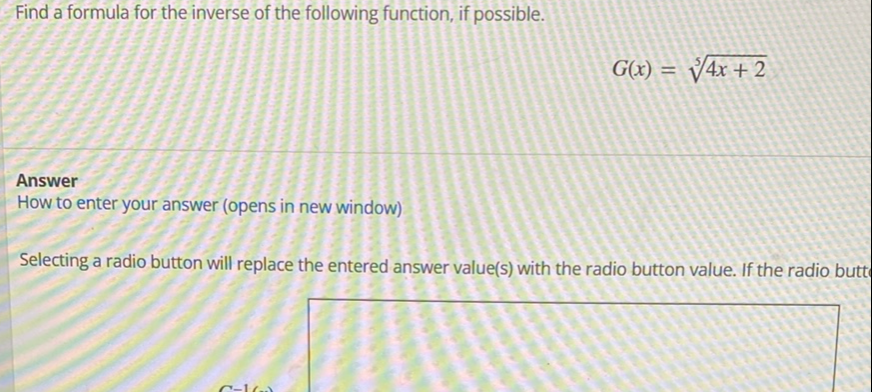
Q. Find a formula for the inverse of the following function, if possible.

\newline

G(x)=\sqrt[5]{4 x+2}

Understand Goal: Understand the function and the goal. $\newline$ We are given the function $G(x) = \sqrt[5]{4x+2}$ , and we need to find its inverse. The inverse function will take the output of $G$ and return the input $x$ .
Set Equation Equal: Set $G(x)$ equal to $y$ for convenience. $\newline$ Let $y = G(x)$ , so we have $y = \sqrt[5]{4x+2}$ .
Swap $x$ and $y$ : Swap $x$ and $y$ to begin finding the inverse. $\newline$ To find the inverse, we switch the roles of $x$ and $y$ . This gives us $x = \sqrt[5]{4y+2}$ .
Isolate y Term: Isolate the term containing $y$ . To solve for $y$ , we need to get rid of the fifth root. We do this by raising both sides of the equation to the power of $5$ . This gives us $x^5 = (\sqrt[5]{4y+2})^5$ .
Simplify Equation: Simplify the equation. $\newline$ When we raise the fifth root to the power of $5$ , they cancel each other out, leaving us with $x^5 = 4y+2$ .
Solve for y: Solve for y. $\newline$ Now we need to isolate $y$ . We do this by subtracting $2$ from both sides and then dividing by $4$ . This gives us $(x^5 - 2)/4 = y$ .
Write Inverse Function: Write the inverse function. $\newline$ The inverse function, which we can denote as $G^{-1}(x)$ , is then $G^{-1}(x) = \frac{x^5 - 2}{4}$ .

More problems from Power rule

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant