AI tutor
Full solution
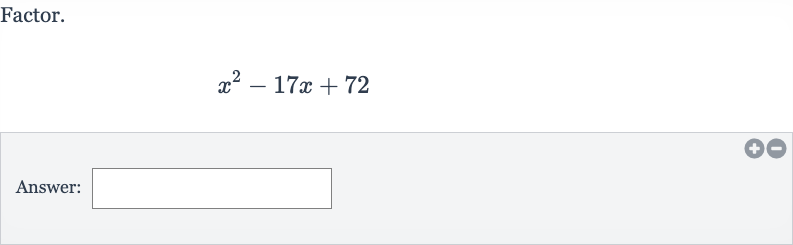
Q. Factor.Answer:
- Identify Factors: To factor the quadratic expression , we need to find two numbers that multiply to (the constant term) and add up to (the coefficient of the term).
- Find Correct Pair: We list pairs of factors of and check which pair adds up to :
and ()
and ()
and ()
and ()
and ()
and ()
We notice that none of the pairs add up to , but if we consider negative pairs, we find that and multiply to and add up to . - Use Negative Pairs: Now we can write the quadratic expression as a product of two binomials using the numbers and :.
- Write as Binomials: To check our work, we can use the FOIL method (First, Outer, Inner, Last) to expand the binomials and verify that we get the original expression:.
More problems from Solve complex trigonomentric equations
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help