AI tutor
Full solution
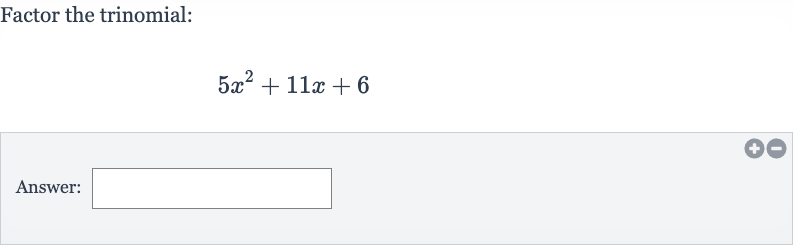
Q. Factor the trinomial:Answer:
- Identify Structure: Identify the structure of the trinomial.The trinomial is in the form , where , , and .
- Find Multiplying Numbers: Look for two numbers that multiply to () and add up to ().We need to find two numbers that multiply to and add up to . The numbers and fit this requirement because and .
- Rewrite Middle Term: Rewrite the middle term using the two numbers found in Step .The trinomial can be rewritten as .
- Factor by Grouping: Factor by grouping.Group the terms into two pairs: and .
- Factor out Common Factor: Factor out the greatest common factor from each group.From the first group , factor out to get .From the second group , factor out to get .
- Write Final Factored Form: Write down the final factored form.Since both groups contain the common factor , the trinomial can be factored as .
More problems from Multiply integers
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help