AI tutor
Full solution
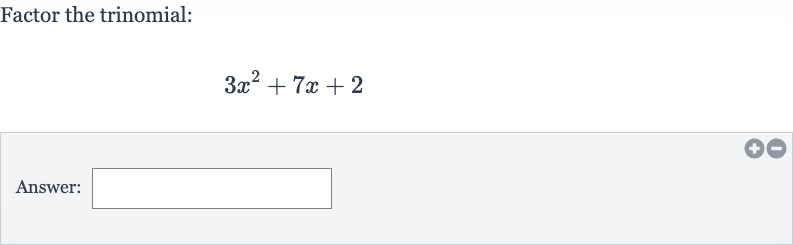
Q. Factor the trinomial:Answer:
- Identify , , : Identify , , and in the trinomial . Compare with .
- Find two numbers: Find two numbers whose product is () and whose sum is ().We need to find two numbers that multiply to and add up to .The numbers and satisfy these conditions because:
- Rewrite middle term: Rewrite the middle term using the two numbers found in Step .We can express as .So, the trinomial can be rewritten as .
- Factor by grouping: Factor by grouping.Group the terms into two pairs: and .Factor out the common factor from each pair.From the first pair, we can factor out : .From the second pair, we can factor out : .Now we have .
- Factor out common binomial: Factor out the common binomial factor .We can now factor out from both terms.The factored form is .