AI tutor
Full solution
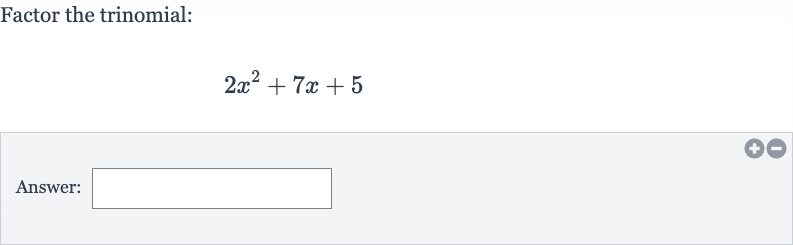
Q. Factor the trinomial:Answer:
- Identify trinomial: Identify the trinomial to be factored, which is .
- Find suitable numbers: Look for two numbers that multiply to give the product of the coefficient of term (which is ) and the constant term (which is ), and add up to the coefficient of the term (which is ).
- Determine numbers: The two numbers that fit the criteria from Step are and , since and .
- Rewrite middle term: Write the middle term as the sum of two terms using the numbers found in Step : . becomes .
- Factor by grouping: Factor by grouping. Group the first two terms together and the last two terms together: .
- Factor out common factor: Factor out the greatest common factor from each group. From the first group, factor out , and from the second group, factor out ..
- Final factored form: Since both groups contain the common factor , factor this out to get the final factored form..
More problems from Multiply integers
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help