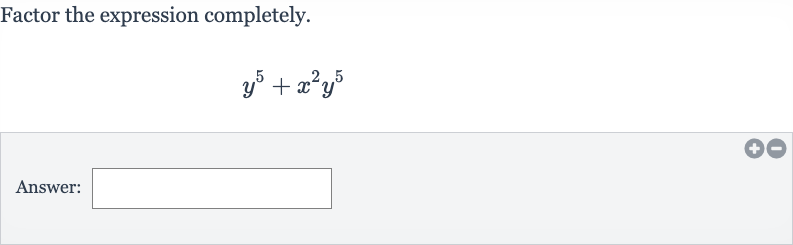AI tutor
Full solution
Q. Factor the expression completely.Answer:
- Identify common factors: Identify common factors in both terms.Both terms and have a common factor of .
- Factor out common factor: Factor out the common factor from both terms.We can factor out of both terms to get .
- Check for further factorization: Check if the remaining expression inside the parentheses can be factored further.The expression cannot be factored further over the real numbers because it is not a difference of squares and has no common factors.
- Write final factored form: Write the final factored form.The completely factored form of the expression is .
More problems from Sin, cos, and tan of special angles
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help