AI tutor
Full solution
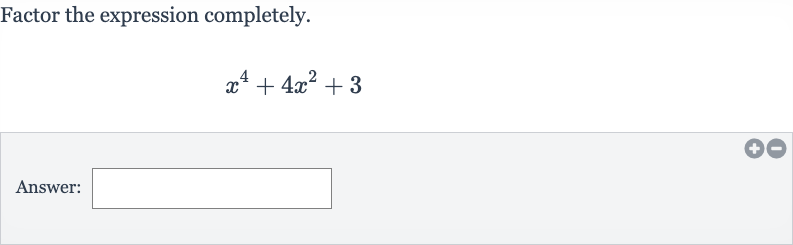
Q. Factor the expression completely.Answer:
- Identify Structure: Identify the structure of the expression.The given expression is , which resembles a quadratic in form, where is the variable.
- Substitute Variable: Substitute for .\ Let . Then the expression becomes .
- Factor Quadratic: Factor the quadratic expression.We need to find two numbers that multiply to and add up to . These numbers are and .So, can be factored as .
- Substitute Back: Substitute back for . Replace with in the factors to get .
- Check Further Factoring: Check if further factoring is possible.Both and are sums of squares and cannot be factored further over the real numbers.
More problems from Evaluate integers raised to rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help