AI tutor
Full solution
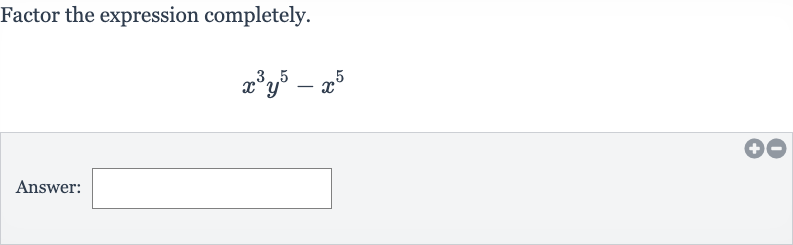
Q. Factor the expression completely.Answer:
- Identify GCF: Identify the greatest common factor (GCF) of the terms in the expression.The GCF of and is , since is the highest power of that divides both terms.
- Factor out GCF: Factor out the GCF from the expression.We can write the expression as .
- Rewrite as product: Rewrite the expression as a product of the GCF and the remaining terms.The factored expression is .
- Check for common factors: Check the factored expression to ensure it is fully factored and that there are no common factors remaining in the terms inside the parentheses.Since and do not share any common factors, the expression inside the parentheses cannot be factored further.
More problems from Find trigonometric ratios using reference angles
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help