AI tutor
Full solution
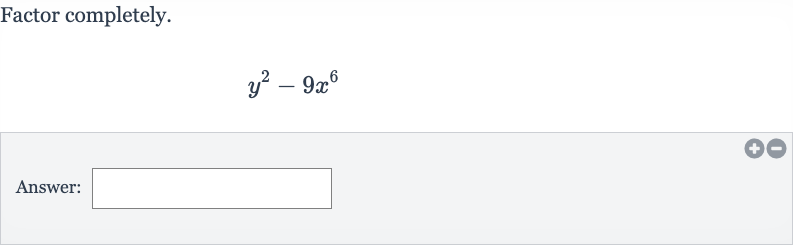
Q. Factor completely.Answer:
- Recognize as difference of squares: Recognize the expression as a difference of squares.A difference of squares is a binomial of the form , which factors into .Here, is a perfect square and is also a perfect square because is a perfect square and is a perfect square .
- Write expression as difference of squares: Write the expression as a difference of squares. can be written as .
- Apply difference of squares formula: Apply the difference of squares formula.Using the formula , we get:.
- Check for additional factoring: Check for any additional factoring.The terms and are not factorable further with real numbers, so the expression is now completely factored.
More problems from Multiply and divide rational expressions
QuestionGet tutor help