AI tutor
Full solution
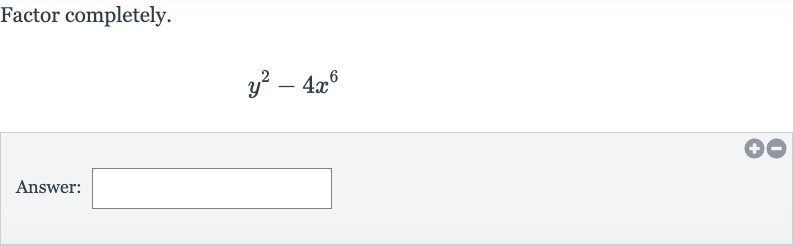
Q. Factor completely.Answer:
- Recognize as difference of squares: Recognize the expression as a difference of squares.A difference of squares is a binomial of the form , which factors into .Here, is a perfect square and is also a perfect square since .
- Write expression as difference: Write the expression as a difference of squares.Now we can apply the difference of squares formula.
- Factor using formula: Factor the expression using the difference of squares formula.This is the completely factored form of the expression.
More problems from Multiply and divide rational expressions
QuestionGet tutor help