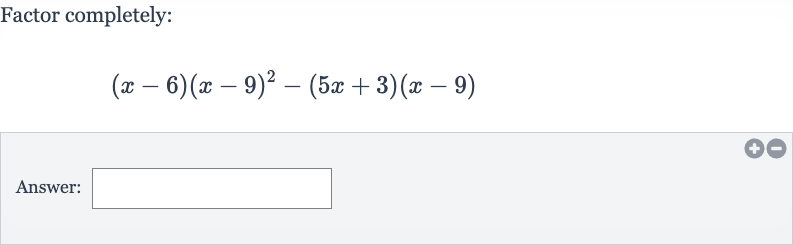AI tutor
Full solution
Q. Factor completely:Answer:
- Recognize common factor: First, we recognize that both terms have a common factor of . We can factor out of both terms.
- Factor out : The expression becomes .
- Distribute and expand: Next, we distribute into the second term, which gives us .
- Simplify inside brackets: Now we expand the term to get .
- Combine like terms: Simplify the expression inside the brackets to get .
- Find factors of : Combine like terms inside the brackets to get .
- Factor quadratic expression: Now we look for factors of that add up to . The numbers and fit this requirement since and .
- Final completely factored form: We can now factor the quadratic expression to get .
- Final completely factored form: We can now factor the quadratic expression to get .This is the completely factored form of the original expression.