Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Factor completely: (8x+1)^(2)-(x-2)^(2) Answer:

Factor completely:\newline(8x+1)2−(x−2)2 (8 x+1)^{2}-(x-2)^{2} \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Factor polynomialsright chevron icon

Full solution

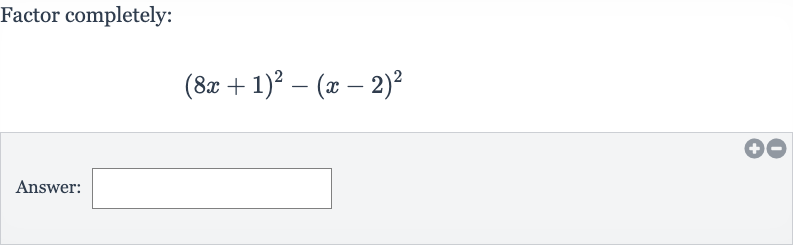
Q. Factor completely:\newline(8x+1)2−(x−2)2 (8 x+1)^{2}-(x-2)^{2} \newlineAnswer:
  1. Recognize as difference of squares: Recognize the expression as a difference of squares. The given expression is in the form of a2−b2a^2 - b^2, which can be factored into (a+b)(a−b)(a + b)(a - b). Here, a=(8x+1)a = (8x + 1) and b=(x−2)b = (x - 2).
  2. Apply formula: Apply the difference of squares formula.\newlineUsing the formula (a+b)(a−b)(a + b)(a - b), we substitute aa and bb with (8x+1)(8x + 1) and (x−2)(x - 2), respectively.\newlineSo, the factored form is ((8x+1)+(x−2))((8x+1)−(x−2))((8x + 1) + (x - 2))((8x + 1) - (x - 2)).
  3. Simplify each binomial: Simplify each binomial.\newlineFirst binomial: (8x+1)+(x−2)=8x+x+1−2=9x−1(8x + 1) + (x - 2) = 8x + x + 1 - 2 = 9x - 1.\newlineSecond binomial: (8x+1)−(x−2)=8x−x+1+2=7x+3(8x + 1) - (x - 2) = 8x - x + 1 + 2 = 7x + 3.
  4. Write final factored form: Write the final factored form.\newlineThe expression is now factored completely as (9x−1)(7x+3)(9x - 1)(7x + 3).

More problems from Factor polynomials

Question
Find the greatest common factor.\newline9v3,6v39v^3, 6v^3\newline\newlineWrite your answer as a constant times a product of single variables raised to exponents.\newline‾\underline{\hspace{1cm}}
Get tutor helpright-arrow

Posted 2 months ago

Question
Factor out the greatest common factor. If the greatest common factor is 11, just retype the polynomial.\newline6x3+9x26x^3 + 9x^2\newline______
Get tutor helpright-arrow

Posted 3 months ago

Question
Factor.\newlinek2+9k+18k^2 + 9k + 18\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Factor.\newline9j2−169j^2 - 16\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Factor.\newlinej3+2j2+5j+10j^3 + 2j^2 + 5j + 10
Get tutor helpright-arrow

Posted 3 months ago

Question
Factor x4+6x2+9x^4 + 6x^2 + 9 completely.\newlineAll factors in your answer should have integer coefficients.\newline______
Get tutor helpright-arrow

Posted 3 months ago

Question
Factor.\newlinez2+13z+22z^2 + 13z + 22\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Simplify the expression: \newline5x+9x−4x−2x5x + 9x - 4x - 2x \newline______
Get tutor helpright-arrow

Posted 4 months ago

Question
3−323 - 3^2
Get tutor helpright-arrow

Posted 4 months ago

Question
5−525 - 5^2
Get tutor helpright-arrow

Posted 2 months ago

View all (193)