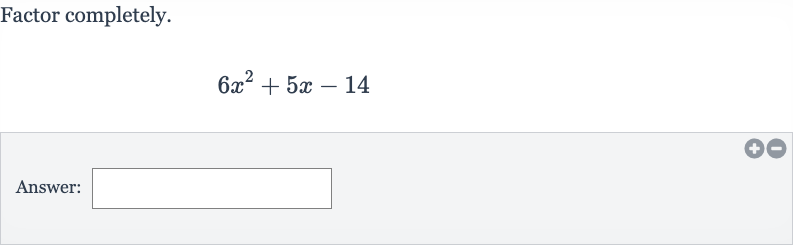
Factor completely. 6x^(2)+5x-14 Answer:

Question

Factor completely.  6x^(2)+5x-14 Answer:

Bytelearn · Accepted Answer

Identify Coefficients: Identify the coefficients of the quadratic expression. The quadratic expression is 6x^2 + 5x - 14. Here, the coefficient of x^2 (a) is 6, the coefficient of x (b) is 5, and the constant term (c) is -14.Find Factor Pairs: Find two numbers that multiply to ac (6 * -14 = -84) and add up to b (5). We need to find two numbers that multiply to -84 and add up to 5. After checking possible factor pairs of -84, we find that 12 and -7 multiply to -84 and add up to 5.Rewrite Middle Term: Rewrite the middle term using the two numbers found in Step 2. We can express 5x as 12x - 7x, which are the two numbers that add up to 5 and multiply to -84. So, the expression becomes 6x^2 + 12x - 7x - 14.Factor by Grouping: Factor by grouping. Now we group the terms to factor by grouping: (6x^2 + 12x) - (7x + 14). We can factor out a common factor of 6x from the first group and -7 from the second group: 6x(x + 2) - 7(x + 2).Factor out Common Factor: Factor out the common binomial factor. Since both groups contain the common binomial factor (x + 2), we can factor it out: (6x - 7)(x + 2).

Factor completely. $\newline$ $6 x^{2}+5 x-14$ $\newline$ Answer:

Full solution

More problems from Factor polynomials

Related topics

Factor completely.\newline6x2+5x−14 6 x^{2}+5 x-14 6x2+5x−14\newlineAnswer:

Factor completely. $\newline$ $6 x^{2}+5 x-14$ $\newline$ Answer: