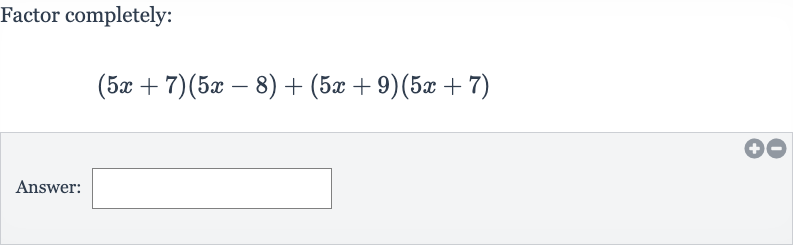AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Factor completely:Answer:
Full solution
Q. Factor completely:Answer:
- Expand Expression: Expand the given expression.We have the expression . To simplify, we first need to expand each set of parentheses by using the distributive property (also known as the FOIL method for binomials).First, expand :Next, expand :Now, add the expanded forms together:
- Combine Like Terms: Combine like terms.After expanding, we combine like terms to simplify the expression further.= =
- Factor by Grouping: Factor by grouping (if possible).Looking at the simplified expression , we try to factor by grouping. However, the coefficients do not have a common factor other than , and the expression does not appear to be factorable by grouping.
- Check Factorability: Check if the expression is factorable.We need to check if the trinomial can be factored. For a trinomial to be factorable, there must be two numbers that multiply to (in this case, ) and add up to (in this case, ). After checking, we find that there are no two integers that satisfy these conditions for the given trinomial. Therefore, the expression is already in its simplest form and cannot be factored further.
