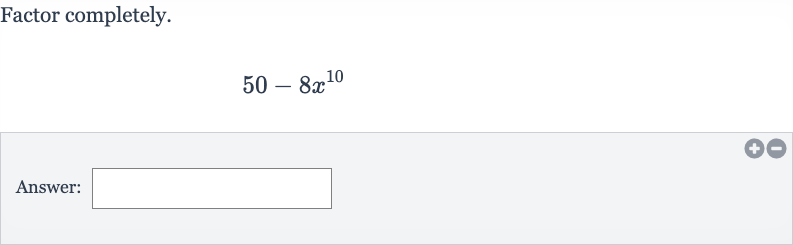
Factor completely. 50-8x^(10) Answer:

Question

Factor completely.  50-8x^(10) Answer:

Bytelearn · Accepted Answer

Identify GCF: Identify the greatest common factor (GCF) of the terms in the expression 50 - 8x^(10). The GCF of 50 and 8 is 2. However, since 8 is a multiple of 2 and we have an x term with a power of 10, we should look for the GCF that includes the variable as well. The GCF that includes the variable is 2x^(10) since x^(10) is the highest power of x present, but we cannot use x^(10) as a factor because it is not a factor of the constant term 50. Therefore, the correct GCF is just 2.Factor out GCF: Factor out the GCF from the expression. 2(25 - 4x^(10)) Check to ensure that when we distribute the 2 back into the parentheses, we get the original expression. 2 * 25 = 50 2 * (-4x^(10)) = -8x^(10) The original expression is correctly factored.Check for Further Factoring: Check if the expression inside the parentheses can be factored further. The expression 25 - 4x^(10) is a difference of squares because it can be written as (5^2) - (2x^5)^2. We can factor a difference of squares using the identity a^2 - b^2 = (a + b)(a - b).Apply Difference of Squares: Apply the difference of squares identity to factor the expression inside the parentheses. (5 + 2x^5)(5 - 2x^5) Ensure that when we square the terms 5 and 2x^5, we get the original terms inside the parentheses. (5)^2 = 25 (2x^5)^2 = 4x^(10) The factoring is correct.Combine GCF with Factored Form: Combine the GCF with the factored form of the expression inside the parentheses to get the final factored form. 2(5 + 2x^5)(5 - 2x^5) Check one last time to ensure that when we distribute the 2 into the factored form and then multiply the binomials, we get the original expression.

Factor completely. $\newline$ $50-8 x^{10}$ $\newline$ Answer:

Full solution

More problems from Factor polynomials

Related topics

Factor completely.\newline50−8x10 50-8 x^{10} 50−8x10\newlineAnswer:

Factor completely. $\newline$ $50-8 x^{10}$ $\newline$ Answer: