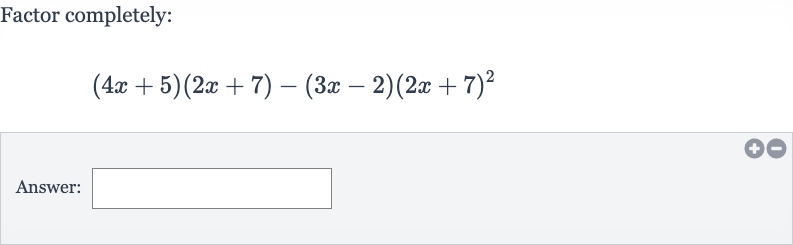Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Factor completely: (4x+5)(2x+7)-(3x-2)(2x+7)^(2) Answer:

Factor completely:\newline(4x+5)(2x+7)−(3x−2)(2x+7)2 (4 x+5)(2 x+7)-(3 x-2)(2 x+7)^{2} \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Transformations of quadratic functionsright chevron icon

Full solution

Q. Factor completely:\newline(4x+5)(2x+7)−(3x−2)(2x+7)2 (4 x+5)(2 x+7)-(3 x-2)(2 x+7)^{2} \newlineAnswer:
  1. Distribute common factor: Distribute the common factor (2x+7)(2x+7) in the expression.\newlineWe notice that (2x+7)(2x+7) is a common factor in both terms of the expression. We can factor it out to simplify the expression.\newline(4x+5)(2x+7)−(3x−2)(2x+7)(2x+7)(4x+5)(2x+7) - (3x-2)(2x+7)(2x+7)
  2. Apply distributive property: Apply the distributive property to factor out (2x+7)(2x+7). We can write the expression as (2x+7)(2x+7) multiplied by the difference of the two terms. (2x+7)[(4x+5)−(3x−2)(2x+7)](2x+7)[(4x+5) - (3x-2)(2x+7)]
  3. Expand second term: Expand the second term inside the brackets.\newlineWe need to multiply (3x−2)(3x-2) by (2x+7)(2x+7) to simplify the expression inside the brackets.\newline(2x+7)[(4x+5)−((3x−2)(2x+7))](2x+7)[(4x+5) - ((3x-2)(2x+7))]
  4. Perform multiplication: Perform the multiplication (3x−2)(2x+7)(3x-2)(2x+7). We use the FOIL method to expand the product. (3x−2)(2x+7)=3x(2x)+3x(7)−2(2x)−2(7)=6x2+21x−4x−14=6x2+17x−14(3x-2)(2x+7) = 3x(2x) + 3x(7) - 2(2x) - 2(7) = 6x^2 + 21x - 4x - 14 = 6x^2 + 17x - 14
  5. Substitute expanded term: Substitute the expanded term back into the expression.\newlineNow we replace the expanded term in the expression.\newline(2x+7)[(4x+5)−(6x2+17x−14)](2x+7)[(4x+5) - (6x^2 + 17x - 14)]
  6. Distribute negative sign: Distribute the negative sign to the terms inside the brackets.\newlineWe need to subtract the entire expanded term from (4x+5)(4x+5).\newline(2x+7)[4x+5−6x2−17x+14](2x+7)[4x + 5 - 6x^2 - 17x + 14]
  7. Combine like terms: Combine like terms inside the brackets.\newlineWe combine the xx terms and the constant terms.\newline(2x+7)[−6x2+(4x−17x)+(5+14)](2x+7)[-6x^2 + (4x - 17x) + (5 + 14)]\newline(2x+7)[−6x2−13x+19](2x+7)[-6x^2 - 13x + 19]
  8. Expression factored completely: The expression is now factored completely. We have factored the expression completely, and there are no common factors or further factoring that can be done. (2x+7)(−6x2−13x+19)(2x+7)(-6x^2 - 13x + 19)

More problems from Transformations of quadratic functions

Question
Solve by completing the square.\newlinem2−10m−29=0m^2 - 10m - 29 = 0\newlineWrite your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.\newline`m` = ____ or `m` = _____
Get tutor helpright-arrow

Posted 8 months ago

Question
Find g(x) g(x) , where g(x) g(x) is the translation 5 5 units up of f(x)=x2 f(x)=x^2 .\newlineWrite your answer in the form a(x–h)2+k a(x–h)^2+k , where a a , h h , and k k are integers.\newlineg(x)= g(x)= ____
Get tutor helpright-arrow

Posted 7 months ago

Question
What is the range of this quadratic function?\newliney=x2−4x+4y = x^2 - 4x + 4\newlineChoices:\newline{y∣y≥2}\left\{y \mid y \geq 2\right\}\newline{y∣y≤0}\left\{y \mid y \leq 0\right\}\newline{y∣y≥0}\left\{y \mid y \geq 0\right\}\newlineall real numbers\text{all real numbers}
Get tutor helpright-arrow

Posted 5 months ago

Question
Write the equation of the parabola that passes through the points (1,0)(1,0), (2,0)(2,0), and (3,–16)(3,\text{–}16). Write your answer in the form y=a(x–p)(x–q)y = a(x – p)(x – q), where aa, pp, and qq are integers, decimals, or simplified fractions.\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.\newlinef2+8f+_____f^2 + 8f + \_\_\_\_\_
Get tutor helpright-arrow

Posted 5 months ago

Question
Solve for h h .\newlineh2+39h=0 h^2 + 39h = 0 \newline\newlineWrite each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.\newlineh= h = ____\newline
Get tutor helpright-arrow

Posted 5 months ago

Question
Write a quadratic function with zeros −9-9 and −7-7.\newlineWrite your answer using the variable xx and in standard form with a leading coefficient of 11.\newlinef(x)=_____f(x) = \_\_\_\_\_
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the equation of the axis of symmetry for the parabola y=x2y = x^2. \newlineSimplify any numbers and write them as proper fractions, improper fractions, or integers.\newline‾\underline{\hspace{3cm}}
Get tutor helpright-arrow

Posted 4 months ago

Question
Find g(x)g(x), where g(x)g(x) is the translation 88 units up of f(x)=x2f(x) = x^2.\newlineWrite your answer in the form a(x–h)2+ka(x – h)^2 + k, where aa, hh, and kk are integers.\newlineg(x)=g(x) = ______\newline
Get tutor helpright-arrow

Posted 4 months ago

Question
Solve for xx.\newlinex2=1x^2 = 1\newline\newlineWrite your answer in simplified, rationalized form.\newlinex=x = ______ or x=x = ______\newline
Get tutor helpright-arrow

Posted 5 months ago

View all (96)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant